Ш¬ШіШӘШ§Шұ
ШҜШұШўЩ…ШҜЫҢ ШЁШұ Ъ©ШЁЫҢШіЩҮ ЩҲ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ - 1
- Ш¬ШіШӘШ§Шұ
- ЩҶЩ…Ш§ЫҢШҙ Ш§ШІ ШҙЩҶШЁЩҮ, 08 ШӘЫҢШұ 1392 18:34
- Ш¶ЫҢШ§ШЎвҖҢШ§Щ„ШҜЫҢЩҶ ШӘШұШ§ШЁЫҢ
- ШЁШ§ШІШҜЫҢШҜ: 13999
В Ш¶ЫҢШ§ШЎвҖҢШ§Щ„ШҜЫҢЩҶ ШӘШұШ§ШЁЫҢ
Ш§ЪҜШұ ШІЩ…Ш§ЩҶ ЪҜШұШҜШҙ ШІЩ…ЫҢЩҶ ШЁЩҮ ШҜЩҲШұ Ш®ЩҲШұШҙЫҢШҜ ЫҢШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜЩӮЫҢЩӮШЈ 365 ШұЩҲШІ ШӘЩ…Ш§Щ… ШЁЩҲШҜШҢ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ЩҮЫҢЪҶ ЩҶЫҢШ§ШІЫҢ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЩҲ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢвҖҢЩҮШ§ЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ЩҶШЁЩҲШҜ. ЩҲЩ„ЫҢ Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ ЫҢШ§ Щ…ШҜШӘ ШІЩ…Ш§ЩҶЫҢ Ъ©ЩҮ ШІЩ…ЫҢЩҶ ШЁЩҮ ШҜЩҲШұ Ш®ЩҲШұШҙЫҢШҜ Щ…ЫҢвҖҢЪҶШұШ®ШҜ Ш§ЩҶШҜЪ©ЫҢ ШЁЫҢШҙвҖҢШӘШұ Ш§ШІ 365 ШұЩҲШІ Ш§ШіШӘШҢ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ Ш§ЫҢЩҶ Ъ©ШіШұЫҢ Ш§Ш¶Ш§ЩҒЫҢ ШіШ§Щ„ ШЁШ§ ЪҜШ°ШҙШӘ ЪҶЩҶШҜЫҢЩҶ ШіШ§Щ„ ШӘШҙЪ©ЫҢЩ„ ЫҢЪ© ШұЩҲШІ Ъ©Ш§Щ…Щ„ ШұШ§ Щ…ЫҢвҖҢШҜЩҮШҜШҢ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜШұ ЪҶЩҶЫҢЩҶ ШіШ§Щ„ЫҢ ШЁЩҮ Ш¬Ш§ЫҢ 365 ШұЩҲШІ ЩҲ Ъ©ШіШұЫҢ Ш§ШІ ШұЩҲШІ 366 ШұЩҲШІ Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ШЁЩҮ ЪҶЩҶЫҢЩҶ ШіШ§Щ„ЫҢ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Щ…ЫҢвҖҢЪҜЩҲЫҢЩҶШҜ. Ш§ШІШіЩҲЫҢ ШҜЫҢЪҜШұ Ш·ЩҲЩ„ ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ (Ш§Ш№ШӘШҜШ§Щ„ЫҢ) Щ…ЩӮШҜШ§ШұЫҢ Ш§ШіШӘ Щ…ШӘШәЫҢШұ Ъ©ЩҮ ШіШ§Щ„ ШЁЩҮ ШіШ§Щ„ ЩҒШұЩӮ Щ…ЫҢвҖҢЪ©ЩҶШҜ ЩҲ ШЁШұШ§ЫҢ ШЁЩҮ ШҜШіШӘ ШўЩҲШұШҜЩҶ Ш·ЩҲЩ„ ЩҲШ§ЩӮШ№ЫҢ ЩҲ ШҜЩӮЫҢЩӮ ЩҮШұ ШіШ§Щ„ ЩҶЫҢШ§ШІ ШЁЩҮ ШұШөШҜ ЩҮШұ ШіШ§Щ„ЩҮ Ш®ЩҲШұШҙЫҢШҜ Ш§ШіШӘ. ШЁШ§ ЩҲШ¬ЩҲШҜ Ш§ЫҢЩҶ Ш§ШІ ШІЩ…Ш§ЩҶвҖҢЩҮШ§ЫҢ ШҜЩҲШұ ШӘШ§Ъ©ЩҶЩҲЩҶ Щ…ШұШҜЩ… ШЁШұШ§ЫҢ ШҜШұ ШҜШіШӘ ШҜШ§ШҙШӘЩҶ ШӯШіШ§ШЁ ШІЩ…Ш§ЩҶ ЫҢШ§ ШӘЩҶШёЫҢЩ… ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢШҢ ШЁЩҲЫҢЪҳЩҮ ШЁШұШ§ЫҢ ЫҢЪ© Щ…ШҜШӘ Ш·ЩҲЩ„Ш§ЩҶЫҢ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШӘШ№ЫҢЫҢЩҶ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ Ш§ЩӮШҜШ§Щ… Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ Ъ©ЩҮ Ъ©ЩҮЩҶвҖҢШӘШұЫҢЩҶ ЩҶЩ…ЩҲЩҶЩҮ ШўЩҶ Щ…ШҜШӘ 365 ШұЩҲШІ ЩҲ ЫҢЪ© ЪҶЩҮШ§ШұЩ… ШұЩҲШІ Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ ЩӮШҜЫҢЩ… Щ…ШЁЩҶШ§ЫҢ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШӘЩҶШёЫҢЩ… ШӘЩӮЩҲЫҢЩ…вҖҢЩҮШ§ЫҢЫҢ ЪҶЩҲЩҶ ШӘЩӮЩҲЫҢЩ… ШұЩҲЩ…ЫҢШҢ ШӘЩӮЩҲЫҢЩ… ШЁШ§ШЁЩ„ЫҢ ЫҢШ§ ШіЩ„ЩҲЪ©ЫҢ ЩҲ Ш§ШіЪ©ЩҶШҜШұЫҢ ЩҲ ШӯШӘЫҢ ШӘЩӮЩҲЫҢЩ… Щ…ЫҢЩ„Ш§ШҜЫҢ ЪҳЩҲЩ„ЫҢЩҶ ШЁЩҲШҜЩҮ Ш§ШіШӘ. ШЁШҜЫҢЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЪҶЩҶЫҢЩҶ ШӘЩӮЩҲЫҢЩ…вҖҢЩҮШ§ЫҢЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ЩҲ ШӘШ№ЫҢЩҶ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҲ Ш№Ш§ШҜЫҢ ШЁШіЫҢШ§Шұ ШіШ§ШҜЩҮ ЩҲ ШұШ§ШӯШӘ Ш§ШіШӘ ЪҶШұШ§ Ъ©ЩҮВ Ъ©ШіШұЫҢ ЫҢЪ© ЪҶЩҮШ§ШұЩ… ШұЩҲШІ ЫҢШ§ ШҙШҙ ШіШ§Ш№ШӘ ШӘЩ…Ш§Щ… ШҜШұ ЩҮШұ ЪҶЩҮШ§Шұ ШіШ§Щ„ ШӘШҙЪ©ЫҢЩ„ ЫҢЪ© ШұЩҲШІ Ш§Ш¶Ш§ЩҒЫҢ Щ…ЫҢвҖҢШҜЩҮШҜ ЩҲ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШіШ§ШҜЪҜЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШіШ§Щ„ ЪҶЩҮШ§ШұЩ… ШұШ§ Ъ©ШЁЫҢШіЩҮ Ъ©ШұШҜ. ЫҢШ№ЩҶЫҢ Ш§ШІ ЩҮШұ ЪҶЩҮШ§Шұ ШіШ§Щ„ ШіЩҮ ШіШ§Щ„ Ш§ЩҲЩ„ ШіШ§Щ„ 365 ШұЩҲШІЩҮ ЩҲ Ш№Ш§ШҜЫҢ Ш§ШіШӘ ЩҲ ШіШ§Щ„ ЪҶЩҮШ§ШұЩ… ШіШ§Щ„ 366ШұЩҲШІЩҮ ЩҲ Ъ©ШЁЫҢШіЩҮ. ШӘШ§Ш«ЫҢШұ ЪҶЩҶЫҢЩҶ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШӘЩӮЩҲЫҢЩ… ЪҜШұЫҢЪҜЩҲШұЫҢ (Щ…ЫҢЩ„Ш§ШҜЫҢ) ШЁШ§ ЩҲШ¬ЩҲШҜ Ш§ШөЩ„Ш§Шӯ Ш·ЩҲЩ„ ШіШ§Щ„ Ш§ШІ 25/365 ШұЩҲШІ ШЁЩҮ 2425/365 ШұЩҲШІ ШЁШұ Ш§ШіШ§Ші ЫҢЪ© ЩӮШұШ§ШұШҜШ§ШҜ ЩҮЩҶЩҲШІ Ш§ШІ ЩҮШұ ЪҶЩҮШ§Шұ ШіШ§Щ„ Щ…ЫҢЩ„Ш§ШҜЫҢ ШіШ§Щ„ ЪҶЩҮШ§ШұЩ… ШұШ§ Ъ©ШЁЫҢШіЩҮ Щ…ЫҢвҖҢЪҜЫҢШұЩҶШҜ. Щ…ЪҜШұ ШіШ§Щ„ ЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШЁЩҮ ШөШҜ Ш®ШӘЩ… Щ…ЫҢвҖҢШҙЩҲЩҶШҜ Щ…Ш«Щ„ ШіШ§Щ„ 100ШҢ200ЩҲ 500 ЩҲ ШәЫҢШұЩҮ Щ…ЪҜШұ ШіШ§Щ„ 400 Щ…ЫҢЩ„Ш§ШҜЫҢ ЫҢШ§ ШіШ§Щ„вҖҢЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШЁШұ ЪҶЩҮШ§ШұШөШҜ ЩӮШ§ШЁЩ„ ШӘЩӮШіЫҢЩ… ШЁШ§ШҙЩҶШҜ Щ…Ш«Щ„ ШіШ§Щ„ 2000 Щ…ЫҢЩ„Ш§ШҜЫҢ Ъ©ЩҮ Ъ©ШЁЫҢШіЩҮ ШЁЩҮ ШҙЩ…Ш§Шұ Щ…ЫҢвҖҢШўЫҢШҜ. ЪҜШұЪҶЩҮ Ш§ЫҢЩҶ ЩҶЩҲШ№ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ЩҶШ§ЩӮШө ЩҲ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ ШЁШ§ Ш§ЫҢЩҶ ШӯШ§Щ„ ШҜШұ ШӘЩ…Ш§Щ… Ъ©ШҙЩҲШұЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШӘЩӮЩҲЫҢЩ… Щ…ЫҢЩ„Ш§ШҜЫҢ ШұЩҲШ§Ш¬ ШҜШ§ШұШҜ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШұЩҲЫҢЩҮ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Щ…ЫҢвҖҢЪ©ЩҶЩҶШҜ. Ш§Щ…Ш§ ШҜШұ Ш§ЫҢШұШ§ЩҶ Ъ©ШЁЫҢШіЩҮ ЩҲЪ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш§ШІ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ш§ЩҲЩ„ ЩҲШ¶Ш№ ШӘЩӮЩҲЫҢЩ… Ш¬Щ„Ш§Щ„ЫҢ ШҜШұШіШ§Щ„ 458ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (1586Ш§ЫҢШұШ§ЩҶЫҢ вҖ“ ШўШұЫҢШ§ЫҢЫҢ) Щ…ЩҲШұШҜ ШЁШӯШ« ЩҲШӘЩҲШ¬ЩҮ Щ…ЩҶШ¬Щ…Ш§ЩҶ ЩӮШұШ§Шұ ШҜШ§ШҙШӘЩҮ Ш§ШіШӘ ЩҲЩ„ЫҢ ШЁЩҮ ЩҶШҜШұШӘ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ ЩҶЩҲШҙШӘЩҮвҖҢШ§ЫҢ Ш§ШІ ШҜЩҲ Щ…ЩҶШ¬Щ… ШЁШұШ®ЩҲШұШҜ Ъ©ЩҮ ШҜШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш§ШІ ШҙЫҢЩҲЩҮ ЩҲШ§ШӯШҜЫҢ ЩҫЫҢШұЩҲЫҢ Ъ©ШұШҜЩҮ ШЁШ§ШҙЩҶШҜ. ШЁШ§ Ш§ЫҢЩҶ ШӯШ§Щ„В ЩӮШҜЫҢЩ…ЫҢ ШӘШұЫҢЩҶ ШіЩҶШҜ ШҜШұ Щ…ЩҲШұШҜ Ъ©ШЁЫҢШіЩҮ ЩҲ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ ШұШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШҜШұ ЩҶЩҲШҙШӘЩҮвҖҢЩҮШ§ЫҢ Ш№ШЁШҜШ§Щ„ШұШӯЩ…Ш§ЩҶ Ш®Ш§ШІЩҶЫҢ (ШөШ§ШӯШЁ ШІЫҢШ¬ ШіЩҶШ¬ШұЫҢ) ЫҢШ§ЩҒШӘШҢ ШўЩҶШ¬Ш§ Ъ©ЩҮ ШҜЩҲШұЩҮЩ” Ъ©Ш§Щ…Щ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ Ш¬Щ„Ш§Щ„ЫҢ (ШіЩ„Ш·Ш§ЩҶЫҢ) ШұШ§ 220 ШіШ§Щ„ Щ…ЫҢвҖҢШҜШ§ЩҶШҜ Ъ©ЩҮ ШҜШұ ШўЩҶ 53 ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜШҢ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ 53 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш·ЩҲЩ„ 220 ШіШ§Щ„В Щ…ШұЪ©ШЁ Ш§ШІ 8Ъ©ШЁЫҢШіЩҮ 5ШіШ§Щ„ЩҮ ЩҲ45 Ъ©ШЁЫҢШіЩҮ 4ШіШ§Щ„ Ш§ШіШӘШҢ ЪҜШұЪҶЩҮ Ш§ЫҢЩҶ ЩҶЩҲШ№ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШҜШұШіШӘ ЩҶЫҢШіШӘ ЩҲ ШҜШұ ШӯЩӮЫҢЩӮШӘ ШҜШұ ЩҮШұ 220 ШіШ§Щ„ 53 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ Щ…ШұЪ©ШЁ Ш§ШІ 7 Ъ©ШЁЫҢШіЩҮ 5 ШіШ§Щ„ЩҮ ЩҲ 46 Ъ©ШЁЫҢШіЩҮ 4 ШіШ§Щ„ЩҮ Ш§ШіШӘ.
ШЁЩҮ ЩҮЩ…ЫҢЩҶ ЪҜЩҲЩҶЩҮ ШҜШ§ЩҶШҙЩ…ЩҶШҜШ§ЩҶ ЩҲЩ…ЩҶШ¬Щ…Ш§ЩҶ Щ…Ш№ШұЩҲЩҒЫҢ ЪҶЩҲЩҶ: Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ (ЩӮШұЩҶ ЩҮЩҒШӘЩ…)ШҢ ЩӮШ·ШЁ Ш§Щ„ШҜЫҢЩҶ ШҙЫҢШұШ§ШІЫҢ (ЩӮШұЩҶ ЩҮШҙШӘЩ…)ШҢ ШӯШіЩҶ ШЁЩҶ ШӯШіЫҢЩҶ ШҙЩҮЩҶШҙШ§ЩҮ ШіЩ…ЩҶШ§ЩҶЫҢ (ЩӮШұЩҶ ЩҮШҙШӘЩ…)ШҢ Ш§Щ„Шә ШЁЫҢЪ© ЪҜЩҲШұЪ©Ш§ЩҶЫҢ (ЩӮШұЩҶ ЩҶЩҮЩ…)ШҢ ЩҲ ЩӮШ§Ш¶ЫҢ ШІШ§ШҜЩҮ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ (ЩӮШұЩҶ ШҜЩҮЩ…)ШҢ ШҜШұ ШІЫҢШ¬вҖҢЩҮШ§ ЫҢШ§ Ъ©ШӘШ§ШЁвҖҢЩҮШ§ЫҢ Ш®ЩҲШҜ ШҜШұ Щ…ЩҲШұШҜ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЩҮ ШӘЩҒШөЫҢЩ„ ШөШӯШЁШӘ Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ.
Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ Щ…ЫҢШ§ЩҶ ЪҜШұЪҶЩҮ Ш§ШёЩҮШ§ШұШ§ШӘ Ш®Ш§ШІЩҶЫҢ ШҜШұЩ…ЩҲШұШҜ 53 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ ЫҢЪ© ШҜЩҲШұЩҮ 220 ШіШ§Щ„ЫҢ ЩҲ ШӘШ§Ъ©ЫҢШҜ ЩҲЫҢ ШЁШұ Ш§ЫҢЩҶ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ 53В ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ 45ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЫҢ ЩҲ 8 ШЁШ§Шұ Ъ©ШЁЫҢШіШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЫҢ Ш§ШіШӘШҢШЁШ§ Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢ Ш§Щ…ШұЩҲШІЫҢВ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ЩҶЩ…ЫҢ Ш®ЩҲШ§ЩҶШҜ ЩҲ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ ШІЫҢШұ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ш§ШІ 53 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш·ЩҲЩ„ 219 ШіШ§Щ„ ШӘШ№ШҜШ§ШҜ 46 ШЁШ§Шұ ШўЩҶ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҲ ШӘЩҶЩҮШ§ 7 ШЁШ§Шұ ШўЩҶ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ:
Ш¬ШҜЩҲЩ„ Ш§ШӯШӘЩ…Ш§Щ„ЫҢ ШҜЩҲШұЩҮ 220ШіШ§Щ„ЩҮЩ” Ш®Ш§ШІЩҶЫҢ
В
В
|
5 ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|
5 |
9 |
13 |
17 |
21 |
25 |
29 |
*** |
|
34 |
38 |
42 |
46 |
50 |
54 |
58 |
62 |
|
67 |
71 |
75 |
79 |
83 |
87 |
91 |
95 |
|
100 |
104 |
108 |
112 |
116 |
120 |
124 |
128 |
|
В |
|||||||
|
133 |
137 |
141 |
145 |
149 |
153 |
157 |
*** |
|
162 |
166 |
170 |
174 |
178 |
182 |
186 |
190 |
|
195 |
199 |
203 |
207 |
211 |
215 |
219 |
*** |
В
В
ШЁШ§ Ш§ЫҢЩҶ ШӯШ§Щ„ ЩҮЩ…ЫҢЩҶ ШӘЩӮШіЫҢЩ… ШЁЩҶШҜЫҢ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШЁЩҮ ШҜЩҲ ЪҜШұЩҲЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЫҢ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЫҢ ШЁШіЫҢШ§Шұ Щ…ЩҮЩ… Ш§ШіШӘ ЩҲ Щ…ЫҢ ШӘЩҲШ§ЩҶШҜ ШұШ§ЩҮЩҶЩ…Ш§ЫҢЫҢ ШЁШұШ§ЫҢ ШұШіЫҢШҜЩҶ ШЁЩҮ ЫҢЪ© Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢ ШҜШұШіШӘВ ЪҜШұШҜШҜ.
В ЩҮЩ…ЫҢЩҶ Ш·ЩҲШұ ЩҲЩӮШӘЫҢ Ш®ЩҲШ§Ш¬ЩҮВ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШҜШұ ШІЫҢШ¬ Ш®ЩҲШҜ (Щ…Ш№ШұЩҲЩҒ ШЁЩҮ ШІЫҢШ¬ Ш§ЫҢЩ„Ш®Ш§ЩҶЫҢ) Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ШӘЩӮЩҲЫҢЩ… Ш¬Щ„Ш§Щ„ЫҢ ШұШ§ ШЁШұШ§ЫҢ Щ…ШҜШӘ 300 ШіШ§Щ„ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢвҖҢЪ©ЩҶШҜ ШЁШ§ШІ ШҜЩӮЫҢЩӮШ§ ШЁЩҮ ЩҮЩ…ЫҢЩҶ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШӘЩҲШ¬ЩҮ ШҜШ§ШұШҜШҢ Ъ©ЩҮ Ш№ШЁШ§ШұШӘ Ш§ШіШӘ Ш§ШІШ¬ШҜЩҲЩ„ЫҢ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ ЫҢШ§ ЩҮЩ…Ш§ЩҶ Ш¬ШҜЩҲЩ„ Щ…ШҜШ®Щ„ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Щ…Щ„Ъ©ЫҢ (Ш¬Щ„Ш§Щ„ЫҢ):
Ш¬ШҜЩҲЩ„ Щ…ШҜШ®Щ„ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮВ Щ…Щ„Ъ©ЫҢ (Ш¬Щ„Ш§Щ„ЫҢ) ЩҶШ§ЩӮШөЩҮ
В
В
| В |
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
||||
|
2 |
6 |
10 |
14 |
18В В В |
22 В |
26 |
**** |
|||||
|
31 В |
35 В |
39 В |
43 |
47 В |
51 В |
55 |
59 |
|||||
|
64 В |
68 |
72 |
76 В |
80 В |
84 В |
88 |
92 В |
|||||
|
97 В |
101 В |
105 |
109 В |
113 |
117 В |
121 В |
125 В |
|||||
|
130 В |
134 В |
138 В |
142 |
146 В |
150 В |
154 В |
158 В |
|||||
|
163 В |
167 В |
171 |
175 В |
179 В |
183 В |
187 |
**** |
|||||
|
19 |
196 В |
200 В |
204 В |
208 В |
212 В |
216 В |
220 В |
|||||
|
225 В |
229 В |
233 В |
237 |
241 В |
245 |
249 В |
253 В |
|||||
|
258 |
262 В |
266 В |
270 В |
274 В |
278 В |
282 |
286 В |
|||||
|
291 |
295 В |
299 В |
*** В |
*** |
*** В |
В |
||||||
В
В
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ЩҮЩ…Ш§ЩҶ Ш¬ШҜЩҲЩ„ ШҜЩҲШұЩҮ Щ…Ш№ШұЩҲЩҒ 161 ШіШ§Щ„ЩҮ Ш§ШіШӘШҢ ЩҲЩ„ЫҢВ Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ШІ ШіШ§Щ„ ШҜЩҲЩ…В Ш¬Щ„Ш§Щ„ЫҢ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 459 ШҙШұЩҲШ№ ШҙШҜЩҮ Ш§ШіШӘШҢ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШҜЩҲШұЩҮ 161 ШіШ§Щ„ЩҮ ШўЩҶ ШЁЩҮ ШіШ§Щ„ 158 Ш®ШӘЩ… Щ…ЫҢ ШҙЩҲШҜ ЩҶЩҮ ШіШ§Щ„ 161.
ЪҜШұЪҶЩҮ Щ…ЩҶШ¬Щ…Ш§ЩҶ ЩҲ ШӘЩӮЩҲЫҢЩ… ЩҶЪҜШ§ШұШ§ЩҶ Щ…Ш№Ш§ШөШұ Ш§Ъ©Ш«ШұШ§ЩӢ Щ…ЩҶЪ©Шұ ЪҶЩҶЫҢЩҶ Щ…ШіШ§Щ„ЩҮвҖҢШ§ЫҢ ЩҮШіШӘЩҶШҜ ЩҲ Щ…Ш№ШӘЩӮШҜЩҶШҜ Ъ©ЩҮ ШЁШ§ЫҢШҜ ШіШ§Щ„ 162 Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ЩҶЩҮ ШіШ§Щ„ 161. ЩҲЩ„ЫҢ ЩҲШ§ЩӮШ№ЫҢШӘ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШіШ§Щ„ 161 Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ЫҢ Ъ©ЩҮ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШҜШұ ЩҶШёШұ ШҜШ§ШұШҜ ШҜЩӮЫҢЩӮШ§ ШҜШұШіШӘ Ш§ШіШӘ. ЪҶШұШ§ Ъ©ЩҮ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШҜШұ ШІЫҢШ¬ Ш®ЩҲШҜ Ш·ЩҲЩ„ ШіШ§Щ„ ШұШ§ 365 ШұЩҲШІ ЩҲ 5ШіШ§Ш№ШӘ ЩҲ 49 ШҜЩӮЫҢЩӮЩҮ ШЁЩҮ ШҙЩ…Ш§Шұ Щ…ЫҢвҖҢШўЩҲШұШҜ ЫҢШ№ЩҶЫҢ Щ…Ш№Ш§ШҜЩ„ 242361125/365 ШұЩҲШІ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
58804=242361125/. Г— 161В (1
58438=242361125/. Г— 160В (2
663 = 58438 - 58804В (3В В
ЩҲЩ„ЫҢ ЩҮЩ…ЫҢЩҶ 161ШіШ§Щ„ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· Ш§Щ…ШұЩҲШІЫҢ ЫҢШ§ 2422/365 ШұЩҲШІВ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ЩҲ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ ШіШ§Щ„ 162 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. ЪҶШұШ§ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
58438=2422 /365Г— 160
58803=2422 /365Г—161
Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Ъ©ШіШұ Ш§ЫҢЩҶ ШҜЩҲ ШұЩӮЩ… Ш§ШІ ЩҮЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
365 = 58438 - 58803
ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 161 ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ ЩҲ 365 ШұЩҲШІЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.ШӯШ§Щ„ Ш§ЪҜШұШ·ЩҲЩ„ ШіШ§Щ„ 162 ШұШ§ ЩҶЫҢШІ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ЩҶШӯЩҲ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
59169=2422 /365Г—162
В ШҜШұ ШөЩҲШұШӘЫҢ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ ШұЩӮЩ… ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ 161 ШұШ§Ъ©ШіШұ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
366 = 58803 - 59169
ЫҢШ№ЩҶЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁШ§ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ Ш§Щ…ШұЩҲШІЫҢ(2422/365ШұЩҲШІ)ШЁЩҮ Ш¬Ш§ЫҢ ШіШ§Щ„ 161ШіШ§Щ„ 162 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
Ъ©ЩҮ Ш§ЫҢЩҶ Ъ©Ш§Шұ ШұШ§ ШЁЩҮ Ш·ЩҲШұ ШіШ§ШҜЩҮ ШӘШұ Щ…ЫҢ ШӘЩҲШ§ЩҶ ЪҶЩҶЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜ:
В 33 = 128 - 161
34 = 128 - 162
ЩҲ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128ШіШ§Щ„ЩҮ ШіШ§Щ„ 33Ъ©ШЁЫҢШіЩҮ ЩҶЫҢШіШӘ ШЁЩ„Ъ©ЩҮ ШіШ§Щ„ 34 Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· Ш§Щ…ШұЩҲШІЫҢ ШіШ§Щ„ 161 ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В ШӯШ§Щ„ ЩӮШЁЩ„ Ш§ШІ ЩҫШұШҜШ§Ш®ШӘЩҶ ШЁЩҮ ЩҶШӯЩҲЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҲЪ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш§ЫҢЩҶ Ъ©ЩҮ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШұШ§ ШЁШ№ШҜЩҮШ§ Щ…ЩҶШ¬Щ… ШҜЫҢЪҜШұЫҢ ШЁЩҶШ§Щ… ШӯШіЩҶ ШЁЩҶ ШӯШіЫҢЩҶ ШЁЩҶ ШҙЩҮЩҶШҙШ§ЩҮ ШіЩ…ЩҶШ§ЩҶЫҢ ШӘЪ©Щ…ЫҢЩ„ ЩҲШӘШ§ ШіШ§Щ„ 443 Ш®ЩҲШұШҙЫҢШҜЫҢ Ш¬Щ„Ш§Щ„ЫҢ Ш§ШҜШ§Щ…ЩҮ ШҜШ§ШҜЩҮ Ш§ШіШӘ ШЁЩҮШӘШұ Ш§ШіШӘ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ ЩҶШ®ШіШӘ Ш¬ШҜЩҲЩ„ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Ш§ЫҢШҙШ§ЩҶ ШұШ§ ШЁЫҢШ§ЩҲШұЫҢЩ… ЩҲ ЩҫШі Ш§ШІ Щ…ШҙШ§ЩҮШҜЩҮ ШӘЩҒШ§ЩҲШӘ ЩҮШ§ЫҢ Ш§ЫҢЩҶ ШҜЩҲ Ш¬ШҜЩҲЩ„ ЩҲЩ…ШӯШ§ШіШЁЩҮ ШЁЩҮ Щ…ЩҲШ¶ЩҲШ№ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ЩҲШұЩҲШҙ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁЩҫШұШҜШ§ШІЫҢЩ…:
В В В В В В В В В В В В В В В В
Ш¬ШҜЩҲЩ„ Щ…ШҜШ®Щ„ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Щ…Щ„Ъ©ЫҢ ЩҶШ§ЩӮШөЩҮВ В В В В В В В В В В В В В В
ШӘЪ©Щ…ЫҢЩ„ЫҢ ШӯШіЩҶ ШЁЩҶ ШӯШіЫҢЩҶ ШЁЩҶ ШҙЩҮЩҶШҙШ§ЩҮ ШіЩ…ЩҶШ§ЩҶЫҢ ( ШӘШ§ 443 Ш¬Щ„Ш§Щ„ЫҢ)
В
В
| В |
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|||
|
2 |
6 |
10 |
14 |
18В В В |
22 В |
26 |
**** |
||||
|
31 В |
35 В |
39 В |
43 |
47 В |
51 В |
55 |
59 |
||||
|
64 В |
68 |
72 |
76 В |
80 В |
84 В |
88 |
92 В |
||||
|
97 В |
101 В |
105 |
109 В |
113 |
117 В |
121 В |
125 В |
||||
|
130 В |
134 В |
138 В |
142 |
146 В |
150 В |
154 В |
158 В |
||||
|
163 В |
167 В |
171 |
175 В |
179 В |
183 В |
187 |
**** |
||||
|
19 |
196 В |
200 В |
204 В |
208 В |
212 В |
216 В |
220 В |
||||
|
225 В |
229 В |
233 В |
237 |
241 В |
245 |
249 В |
253 В |
||||
|
258 |
262 В |
266 В |
270 В |
274 В |
278 В |
282 |
286 В |
||||
|
291 |
295 В |
299 В |
303 В |
307 |
311 В |
315 |
**** В |
||||
|
320 В |
324 |
328 В |
332 |
336 В |
340 |
344 В |
348 В |
||||
|
353 В |
357 В |
361 В |
365 В |
369 |
373 В |
377 В |
381 В |
||||
|
386 |
390 |
394 |
398 |
402 |
406 |
410 |
414 |
||||
|
419 В |
423 В |
427 |
431 В |
435 В |
439 В |
443 В |
**** В |
||||
В
В
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ЪҜШұЪҶЩҮ ШҜЩҶШЁШ§Щ„ЩҮ Ш¬ШҜЩҲЩ„ 300ШіШ§Щ„ЩҮ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ Ш§ШіШӘ ШЁШ§ Ш§ЫҢЩҶ ШӯШ§Щ„ Ш§ШІ ЩҶШёШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШўЩҶ ШӘЩҒШ§ЩҲШӘ ШҜШ§ШұШҜ. ШЁЩҮ Ш№ШЁШ§ШұШӘ ШҜЫҢЪҜШұ Ш§ЪҜШұ ШЁЩҶШ§ ШЁЩҲШҜ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ШЁШұШ§ШіШ§Ші Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШӘЪ©Щ…ЫҢЩ„ ШҙЩҲШҜ ШҢ ШЁШ§ЫҢШҜ ШЁШ№ШҜ Ш§ШІ ШіШ§Щ„ 315 ЫҢЪ© Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ Щ…ЫҢ ШўЩ…ШҜШӘШ§ ШЁШұШіШҜ ШЁЩҮ ШіШ§Щ„ 319 ЩҲ ЩҫШ§ЫҢШ§ЩҶ ШҜЩҲШұЩҮ ШҜЩҲЩ… 161 ШіШ§Щ„ ЩҲ Щ…Ш¬ШҜШҜШ§ ШҜЩҲШұЩҮ 161 ШіШ§Щ„ЩҮ ШіЩҲЩ… Ш§ШІ ШіШ§Щ„ 324 ШўШәШ§ШІ Щ…ЫҢвҖҢШҙШҜ. ЩҲЩ„ЫҢ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢЩ… Ъ©ЩҮ Ш§ЫҢЩҶ Ш·ЩҲШұ ЩҶЫҢШіШӘ ЩҲ ШҜШұ ШӯЩӮЫҢЩӮШӘ ШӯШіЩҶ ШЁЩҶ ШӯШіЫҢЩҶ ШЁЩҶ ШҙЩҮЩҶШҙШ§ЩҮ ШіЩ…ЩҶШ§ЩҶЫҢ ШҜШұ Ш§ШҜШ§Щ…ЩҮ Ш¬ШҜЩҲЩ„ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ ШЁЩҮ Ш¬Ш§ЫҢ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ 161 ШіШ§Щ„ЩҮ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 128 ШіШ§Щ„ЫҢ ШұШ§ Щ…ШҜЩҶШёШұ ЩӮШұШ§Шұ ШҜШ§ШҜЩҮ Ш§ШіШӘ. ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ЩҶШ®ШіШӘЫҢЩҶ Ш§Ш«Шұ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШұШ§ ШҜШұ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ШӯШіЩҶ ШЁЩҶ ШӯШіЫҢЩҶ ШЁЩҶ ШҙЩҮЩҶШҙШ§ЩҮ ШіЩ…ЩҶШ§ЩҶЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЫҢШ§ЩҒШӘ. ЫҢШ№ЩҶЫҢ ЩҮЩ…Ш§ЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮвҖҢШ§ЫҢВ Ъ©ЩҮ ШҜШұ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ш§Ш®ЫҢШұ ШЁШұШ§ЫҢ ЩҶШ®ШіШӘЫҢЩҶ ШЁШ§Шұ ШІЩҶШҜЩҮ ЫҢШ§ШҜ Ш§ШіШӘШ§ШҜШіЫҢШҜ ШӯШіЩҶ ШӘЩӮЫҢ ШІШ§ШҜЩҮ ШҜШұ Ъ©ШӘШ§ШЁ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш®ЩҲШҜ Щ…Ш·ШұШӯ ШіШ§Ш®ШӘЩҮ ЩҲ ШӘШ§Ъ©ЫҢШҜ Ъ©ШұШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ЩҮШұ 128 ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ 31 ШЁШ§Шұ ШӘЩ…Ш§Щ… Ъ©ШЁЫҢШіЩҮ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ ШӘЩҶШёЫҢЩ… Ш¬ШҜЩҲЩ„ЫҢ ШЁШұШ§ЫҢ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮШҢ ШЁШұШ§ШіШ§Ші ШҙШҙ ЫҢШ§ ЩҮЩҒШӘ ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ШЁШ§ЫҢШҜ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЫҢШ§ЫҢШҜ. ШҜШұШ§ЫҢЩҶ ШөЩҲШұШӘ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
В Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ
В
ЪҶЩҮЩҖЩҖЩҖШ§Шұ ШіЩҖЩҖЩҖШ§Щ„ЩҠ |
ЩҫЩҶШ¬ ШіШ§Щ„ЩҠ |
||||||
|
ЩҖЩҖЩҖЩҖ |
29 |
25 |
21 |
17 |
13 |
9 |
5 |
|
62 |
58 |
54 |
50 |
46 |
42 |
38 |
34 |
|
95 |
91 |
87 |
83 |
79 |
75 |
71 |
67 |
|
128 |
124 |
120 |
116 |
112 |
108 |
104 |
100 |
В
В
В ЪҜШұЪҶЩҮ ЪҜШұЩҲЩҮЫҢ Ш§ШІ ШӘЩӮЩҲЫҢЩ… ЩҶЪҜШ§ШұШ§ЩҶ Щ…Ш№Ш§ШөШұ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ЩҲ 31ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ 128 ШұШ§ ЩӮШ·Ш№ЫҢ ШӘЩ„ЩӮЫҢ Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ Ъ©ЩҮ Ш§ШІ ШўЩҶ Щ…ЫҢШ§ЩҶ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ШІ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ЩҲ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© ЩҲ ЩҶЫҢШІ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ЩҶШ§Щ… ШЁШұШҜШҢ Ъ©ЩҮ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШұШ§ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШҜЩҲШұЩҮ Ъ©Ш§Щ…Щ„ ЩҫШ°ЫҢШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ. ЩҲЩ„ЫҢ ЩҲШ§ЩӮШ№ЫҢШӘ Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮВ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШҜЩҲШұЩҮ Ъ©Ш§Щ…Щ„ЫҢ ЩҶЫҢШіШӘ. ЪҶШұШ§ Ъ©ЩҮ ШЁШ§ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ 2422/365 ШұЩҲШІ ШҜШұ 128 ШіШ§Щ„ Ш№Щ„Ш§ЩҲЩҮ ШЁШұ 31ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮШҢ Щ…ЩӮШҜШ§Шұ Ш§ЩҶШҜЪ©ЫҢ Ш§Ш¶Ш§ЩҒЫҢ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ ШЁШ§ ЪҜШ°ШҙШӘ ШІЩ…Ш§ЩҶ ШӘШҙЪ©ЫҢЩ„ ЫҢЪ© ШұЩҲШІ ЫҢШ§ ЫҢЪ© ШұЩҲШІ Ш§Ш®ШӘЩ„Ш§ЩҒ ШҜШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Щ…ЫҢвҖҢЪҜШұШҜШҜ.
ШӯШ§Щ„ ШЁШұШ§ЫҢ Щ…ШҙШ®Шө ШҙШҜЩҶ Ш§ЫҢЩҶ ШұЩӮЩ… ЫҢШ§ Ъ©ШіШұЫҢ Ш§Ш¶Ш§ЩҒЫҢ ШЁШұ31 ШұЩҲШІШҢ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
В В В 0016 /31 = 2422/. Г— 128
Ъ©ЩҮ ЩҮЩ…ЫҢЩҶ ШұЩӮЩ… Ш§ЩҶШҜЪ© 0016/. ШұЩҲШІ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШЁШ§ ЪҜШ°ШҙШӘ 673 ШіШ§Щ„ ШӘЩҲЩ„ЫҢШҜ ЫҢЪ© ШіШ§Щ„ Ш§Ш®ШӘЩ„Ш§ЩҒ Щ…ЫҢвҖҢШҙЩҲШҜ. ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШіШ§Щ„ 674 ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ ШіШ§Щ„ 673 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ. ШЁШҜЫҢЩҶ ШөЩҲШұШӘ Ъ©ЩҮ ШҜШұШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
0006 /245808=2422 /365Г—673
В 7584 /245442=2422 /365Г—672
366 = 245442 - 245808
ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 673 ЫҢЪ© ШіШ§Щ„ 366 ШұЩҲШІЩҮ ЩҲ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ.
ЪҜЩҒШӘЩҶЫҢ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ©ЫҢ Ш§ШІ ШұЩҲШҙ ЩҮШ§ЫҢ ШӘШҙШ®ЫҢШө Ъ©ШЁЫҢШіЩҮ ЫҢШ§ ШәЫҢШұ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ЫҢЪ© ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ ЩҮЩ…ЫҢЩҶ ШҙЫҢЩҲЩҮЩ” Щ…ШӯШ§ШіШЁЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШ·Шұ Ш§ШіШӘ Ъ©ЩҮ ШЁШұШ§ШіШ§Ші ЫҢЪ© ЩҒШұЩ…ЩҲЩ„ ШіШ§ШҜЩҮ ШЁЩҮ ШҜШіШӘ Щ…ЫҢвҖҢШўЫҢШҜШҢ ЫҢШ№ЩҶЫҢ ЩҒШұЩ…ЩҲЩ„ ШІЫҢШұ:
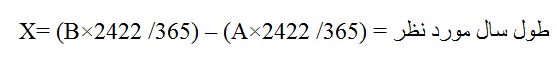
В AВ Ш№ШЁШ§ШұШӘШіШӘ Ш§ШІ Ш·ЩҲЩ„ ШіШ§Щ„ЩҮШ§ЫҢ ШіЩҫШұЫҢ ШҙШҜЩҮ ШӘШ§ ЩҫШ§ЫҢШ§ЩҶ ШіШ§Щ„ Щ…Ш§ЩӮШЁЩ„ ШіШ§Щ„ Щ…ЩҲШұШҜЩҶШёШұ.
B Ш№ШЁШ§ШұШӘ Ш§ШіШӘ Ш§ШІ Ш·ЩҲЩ„ ШіШ§Щ„ ЩҮШ§ЫҢ ШіЩҫШұЫҢ ШҙШҜЩҮ Ш§ШІ Щ…ШЁШҜШ§ ШӘШ§ ЩҫШ§ЫҢШ§ЩҶ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ.
X ЩҶЫҢШІ Ш№ШЁШ§ШұШӘ Ш§ШіШӘ Ш§ШІ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ.
В
ШЁШ§ Ш§ЫҢЩҶ ШӘЩҲШ¶ЫҢШӯ ШҜШұ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШұЩӮЩ…вҖҢЩҮШ§ЫҢ Ъ©ШіШұЫҢ ШЁЩҮ ШӯШіШ§ШЁ ЩҶЩ…ЫҢвҖҢШўЫҢЩҶШҜ ЩҲ Щ…ШӯШ§ШіШЁЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ ШЁШұШ§ЫҢ ШЁЩҮ ШҜШіШӘ ШўЩҲШұШҜЩҶ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҮЩ…ЫҢШҙЩҮ ШЁШұШ§ШіШ§Ші ШұЩӮЩ… ШөШӯЫҢШӯ ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ ШЁШҜЩҲЩҶ ШҜШұ ЩҶШёШұ ЪҜШұЩҒШӘЩҶ Ъ©ШіШұШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ. ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ШҜШұ Щ…ШӯШ§ШіШЁЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ 673 Ш№Щ…Щ„ ШҙШҜ. Ш§ШІ ШіЩҲЫҢ ШҜЫҢЪҜШұ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ЩҲЩӮШӘЫҢ ШҜШұШіШӘ Ш§ШіШӘ Ъ©ЩҮ Щ…ШЁШҜШ§ЫҢЫҢ ЩҲШ¬ЩҲШҜ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ ЫҢШ№ЩҶЫҢ Щ…ШЁШҜШ§ШҜЩӮЫҢЩӮ ЩҲ ШҜШұШіШӘЫҢ Ъ©ЩҮ ШЁШӘЩҲШ§ЩҶ ШЁШ§ ШўЩҶ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШӘШ№ЫҢЫҢЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЩҫШұШҜШ§Ш®ШӘ. ЩҲ ЪҜШұЩҶЩҮ ШӯШӘЩ…Ш§ ШҜШұ ШӘШ№ЫҢЫҢЩҶ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ЫҢШ§ ЩҶШЁЩҲШҜЩҶ ШіШ§Щ„ ШЁЩҮ ЩҶШӘЫҢШ¬ЩҮЩ” ЩҶШ§ШҜШұШіШӘЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШұШіЫҢШҜ.
ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш§ШІ Ш·ШұЫҢЩӮ ЩҮЩ…ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШіШ§ШҜЩҮ Щ…ШӘЩҲШ¬ЩҮ ШҙШҜ Ъ©ЩҮ ЩҶЩҮ ШіШ§Щ„ Ш§ЩҲЩ„ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…ШЁШҜШ§ ШӘЩӮЩҲЫҢЩ… Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ Ш§Щ…ШұЩҲШІЫҢ Ш§ШіШӘ ЩҲЩҶЩҮ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ.
ШЁШұШ§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ Ш§ЪҜШұ Щ…ШЁШҜШ§ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„ Ш§ЩҲЩ„ ШўЩҶ ШЁЩҲШҜ ШЁШ§ЫҢШіШӘЫҢ ШіШ§Щ„ ЩҫЩҶШ¬Щ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ Ъ©ЩҮ ЩҶЫҢШіШӘ ЩҲ ЩҮЫҢЪҶ ЫҢЪ© Ш§ШІ Ъ©ШӘШ§ШЁ ЩҮШ§ ЩҲ Ш¬ШҜЩҲЩ„ ЩҮШ§ЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Щ…Ш№Ш§ШөШұЫҢЩҶ ШіШ§Щ„ ЩҫЩҶШ¬Щ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШұШ§ Ъ©ШЁЫҢШіЩҮ ЩҶЪҜШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ. ЩҲ Ш§ШІ Ш·ШұЩҒЫҢ ШҜШұ Ъ©ШӘШ§ШЁвҖҢЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШҜШұШЁШ§ШұЩҮ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ ШӘШ§ШұЫҢШ® ШӘШөЩҲЫҢШЁ ЩҲ Ш§Ш¬ШұШ§ЫҢ ЩӮШ§ЩҶЩҲЩҶ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш¬ШҜЫҢШҜ ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ ЩҮЩ…ЩҮ Ш¬Ш§ ШіШ§Щ„ 1304 ЫҢШ№ЩҶЫҢ ШіШ§Щ„ ШӘШөЩҲЫҢШЁ ЩҲ Ш§Ш¬ШұШ§ЫҢ ЩӮШ§ЩҶЩҲЩҶ ШӘЩӮЩҲЫҢЩ… Щ…Ш°Ъ©ЩҲШұ ШұШ§ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁЩҮ ШҙЩ…Ш§ШұШўЩҲШұШҜЩҮвҖҢШ§ЩҶШҜ ЩҲ ЩҫЩҶШ¬Щ…ЫҢЩҶ ШіШ§Щ„ ШЁШ№ШҜЫҢ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 1309 ШұШ§ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЩҮ ШҙЩ…Ш§Шұ ШўЩҲШұШҜЩҮвҖҢШ§ЩҶШҜ.
ЩҲЩ„ЫҢ ШҜШұШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш§ШІ Щ…ШЁШҜШ§ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
476275=В 2422 /365 Г—1304
475910=2422 /365Г—1303
365=475910 вҖ“ 476275
ЫҢШ№ЩҶЫҢ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш§ШІ Щ…ШЁШҜШ§ ЩҮШ¬ШұЫҢ ШіШ§Щ„ 1304 ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
ШӯШ§Щ„ Ъ©ЩҮ Ш§ЪҜШұ ЩҮЩ…ЫҢЩҶ ШіШ§Щ„ 1304 ШұШ§ Ш§ШІ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
847 = 457В - 1304
846В = 457В - 1303
309360 =В 2422 /365 Г— 847
308994В =2422 /365В Г—846
366 = 308994 -В 309360
ЩҲ ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁШұ Ш№Ъ©Ші Щ…ШӯШ§ШіШЁЩҮВ ЩӮШЁЩ„ЫҢ Ш§ЫҢЩҶ ШЁШ§Шұ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЫҢЪ© ШіШ§Щ„ 366 ШұЩҲШІЩҮ ЩҲ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
ШӯШ§Щ„ ШіШ§Щ„ 1309 ШұШ§ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ЩҶШӯЩҲ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш§ШІ Щ…ШЁШҜШ§ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
478102В =В В 2422 /365 Г— 1309
477736В =2422 /365 Г—В 1308
366В = 477736 вҖ“ 478102
ЫҢШ№ЩҶЫҢ ШЁШ§ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШіШ§Щ„ 1309 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ. ЩҲЩ„ЫҢ Ш§ЪҜШұ ЩҮЩ…ЫҢЩҶ ШіШ§Щ„ ШұШ§ Ш§ШІ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
852В = 457В -В 1309
851В = 457 -В 1308
311186 =В 2422 /365Г— 852
310821В =В В В В 2422 /365 Г— 851
365 = 310821В - 311186
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ШіШ§Щ„ 1309 ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш§ШіШӘ. ЫҢШ№ЩҶЫҢ ШҜШұ ЩҮЫҢЪҶ ЫҢЪ© Ш§ШІ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁШ§Щ„Ш§ ШҜЩҲ ШіШ§Щ„ 1304 ЩҲ 1309 Ъ©ШЁЫҢШіЩҮ ШҜШұ ЩҶЩ…ЫҢвҖҢШўЫҢЩҶШҜ (ЫҢШ№ЩҶЫҢ ШЁШ§ ЩҮШұ Ъ©ШҜШ§Щ… Ш§ШІ Ш§ЫҢЩҶ Щ…ШЁШҜШ§ЩҮШ§ ЩҒЩӮШ· ЫҢЪ©ЫҢ Ш§ШІ Ш§ЫҢЩҶ ШҜЩҲ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШҜШұ Щ…ЫҢвҖҢШўЫҢШҜ ШҜШұ ШөЩҲШұШӘЫҢ Ъ©ЩҮ Ш·ШЁЩӮ Ш§ШіЩҶШ§ШҜ ЩҲ Щ…ШҜШ§ШұЪ© Щ…ЩҲШ¬ЩҲШҜ ЩҮШұ ШҜЩҲШіШ§Щ„ 1304 ЩҲ 1309 Ъ©ШЁЫҢШіЩҮ ЩҮШіШӘЩҶШҜ)ШҢ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ Ш§ЫҢЩҶ ШҜЩҲ ЩҮЫҢЪҶ Ъ©ШҜШ§Щ… ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶЩҶШҜ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ЩӮШұШ§Шұ ЪҜЫҢШұЩҶШҜ. Ш§Щ„ШЁШӘЩҮ ШҙЩ…Ш§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶЫҢШҜ Ш§ЫҢЩҶ ШўШІЩ…Ш§ЫҢШҙ Шұ Ш§ ШЁШ§ ЩҮШұ ШіШ§Щ„ ШҜЫҢЪҜШұЫҢ Ъ©ЩҮ ШЁШ®ЩҲШ§ЩҮЫҢШҜ Ш§ЩҶШ¬Ш§Щ… ШҜЩҮЫҢШҜ ЩҲЩ„ЫҢ ЩҶШӘЫҢШ¬ЩҮ ЩҮЩ…ЫҢЩҶ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ Ъ©ЩҮ ШҜЫҢШҜЫҢЩ….
Ъ©ЩҮ ШҜШұ ШӯЩӮЫҢЩӮШӘ Ш§ЫҢЩҶ Ш§Ш®ШӘЩ„Ш§ЩҒ ЩҶШ§ШҙЫҢ Ш§ШІ Ш¬Ш§ШЁШ¬Ш§ЫҢЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ш§ШіШӘ ШЁШҜЫҢЩҶ ЪҜЩҲЩҶЩҮ Ъ©ЩҮ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ ЩҒЩӮШ· ЫҢЪ© ШіШ§Щ„ ШҜШұ Щ…ШЁШҜШ§ ШӘШәЫҢЫҢШұ ШЁШҜЩҮЫҢЩ… ШӘШ§ Ш¬Ш§ЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁШ§ЩҮЩ… Ш№ЩҲШ¶ ШҙЩҲШҜ ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢвҖҢЩҮШ§ЫҢ Щ…Ш§ ЩҶШ§ШҜШұШіШӘ Ш§ШІ ШўШЁ ШҜШұ ШЁЫҢШ§ЫҢШҜ.
ШЁЩҮ ЩҮЩ…ЫҢЩҶ Ш№Щ„ШӘ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁШ§Щ„Ш§ ЩҲЩӮШӘЫҢ Щ…ШЁШҜШЈ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§Щ…ШұЩҲШІЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШұШ§ ШіШ§Щ„ Ш§ЩҲЩ„ ЩҮШ¬ШұШӘ ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ… ЫҢШ§ Щ…ШЁШҜШ§ ШўЩҶ ШұШ§ ШіШ§Щ„ Ш§ЩҲЩ„ Ш¬Щ„Ш§Щ„ЫҢ ЫҢШ§В Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ (Щ…Щ„Ъ©ЫҢ) ШҜШұ ЩҶШёШұ ШЁЪҜЫҢШұЫҢЩ… ШЁЩҮ ШҜЩ„ЫҢЩ„ ЩҮЩ…ЫҢЩҶ Ш¬Ш§ШЁШ¬Ш§ЫҢЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬В ШіШ§Щ„ЩҮ ШЁШ§ ЩҮЩ… ШЁШ§ ЩҶШӘШ§ЫҢШ¬ ЩҶШ§ШҜШұШіШӘЫҢ ШұЩҲШЁШұЩҲ Щ…ЫҢ ШҙЩҲЫҢЩ…. ЩҲ ШЁЩҮ Ш®Ш§Ш·Шұ ЩҮЩ…ЫҢЩҶ Ш¬Ш§ШЁШ¬Ш§ЫҢЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ШіШӘ Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ЩҮШұ ШҜЩҲ ШіШ§Щ„ 1304 ЩҲ 1309 Ъ©ШЁЫҢШіЩҮ ШҜШұ ШЁЫҢШ§ЫҢЩҶШҜ ШҜШұ ЫҢЪ©ЫҢ ЩҒЩӮШ· ШіШ§Щ„ 1304 Ъ©ШЁЫҢШіЩҮ ШҜШұ Щ…ЫҢвҖҢШўЫҢШҜ ЩҲ ШҜШұ ШҜЫҢЪҜШұЫҢ ЩҒЩӮШ· ШіШ§Щ„ 1309.
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ Ш§ЪҜШұ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁШ§ШӘ ШұШ§ Ш§ШҜШ§Щ…ЩҮ ШҜЩҮЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜЫҢШҜ Ъ©ЩҮ ЩҲЩӮШӘЫҢ ШіШ§Щ„ Ш§ЩҲЩ„ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШұШ§ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁЩҮ ЩӮШұШ§Шұ ШЁШҜЩҮЫҢЩ… ШЁЩҮ Ш¬Ш§ЫҢ ШіШ§Щ„ 1304 ШіШ§Щ„ 1305 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ ЩҲ ШЁЩҮ ШӘШЁШ№ ШўЩҶ ШіШ§Щ„ 1309ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ЫҢЪ© Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁШ§ШҙШҜ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ. ЩҮЩ…ЫҢЩҶ Ш·ЩҲШұ ЩҲЩӮШӘЫҢ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ ШұШ§ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁЩҮ ЩӮШұШ§Шұ ШҜЩҮЫҢЩ… Ш§ЫҢЩҶ ШЁШ§Шұ ШЁЩҮ Ш¬Ш§ЫҢ ШіШ§Щ„ 1309 ШіШ§Щ„ 1308 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ. ЩҲ Ш§ЫҢЩҶ Ш§ШӘЩҒШ§ЩӮЫҢ Ш§ШіШӘ Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 1440ШіШ§Щ„ЩҮ ЩӮШ§Ш¶ЫҢ ШІШ§ШҜЩҮ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ЩҶЫҢШІ ШұШ® ШҜШ§ШҜЩҮ Ш§ШіШӘ.
ЪҜШұЪҶЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ЩҲ Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ШҜШұ Ъ©Щ„ Ш§ШҙШӘШЁШ§ЩҮ ЩҲ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ ЩҲ ШӘЩӮШіЫҢЩ… ШЁЩҶШҜЫҢ Ш§ЩҲ ШҜШұ Щ…ЩҲШұШҜ ШӘЩӮШіЫҢЩ… Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ ЪҶЩҮШ§ШұВ ШіШ§Щ„ЩҮ ЩҲЩҫЩҶШ¬ ШіШ§Щ„ЩҮ (ШіЩҮ ШҜЩҲШұЩҮ29ШіШ§Щ„ЩҮ ЩҲШЁЩӮЫҢЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ) ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ ШҜШұШіШӘ ШЁШ§ШҙШҜШҢ ШЁШ§ Ш§ЫҢЩҶ ШӯШ§Щ„ Щ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ш¬Ш§Щ„ШЁ ШӘЩҲШ¬ЩҮ ШЁШ§ШҙШҜ ШЁЩҮ ЩҮЩ…ЫҢЩҶ Ш¬ЩҮШӘВ Ш§ЫҢЩҶВ ШұЩҲШ§ЫҢШӘ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ШұШ§ ШҜШұ Щ…ЩҲШұШҜ 349 Ъ©ШЁЫҢШіЩҮ ШҜШұ 1440 ШіШ§Щ„ ШұШ§ Ъ©ЩҮ ШҜШұ ШўЩҶ Ш§ШІ Ш§ЫҢЩҶ 349 ШЁШ§Шұ 305 ШЁШ§ШұШҙ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ШЁЩҲШҜЩҮ ЩҲ 44 ШЁШ§ШұШҙ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ъ©ЩҮ ШЁШ§ШІ Ш§ШІ Ш§ЫҢЩҶ 44 Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ 41 Щ…ШұШӘШЁЩҮвҖҢШ§Шҙ ЩҫШі Ш§ШІ ЩҮЩҒШӘ ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ ЩҲ ШӘЩҶЩҮШ§ ШіЩҮ Щ…ШұШӘШЁЩҮ Ш§Шҙ ЩҫШі Ш§ШІ ШҙШҙ ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮВ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩӮШұШ§Шұ Щ…ЫҢвҖҢЪҜЫҢШұШҜШҢ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШӘЩҶШёЫҢЩ… ШЁЩҮ ШөЩҲШұШӘ ЫҢЪ© Ш¬ШҜЩҲЩ„ Щ…ЩҶШёЩ… ЪҶЩҶЫҢЩҶ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ:
В Ш¬ШҜЩҲЩ„ ЩҫЫҢШҙЩҶЩҮШ§ШҜЫҢ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ЩҲШӘШ·ШЁЫҢЩӮ ШўЩҶ ШЁШ§ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ
В
В
|
В Ъ©ШЁЫҢШіЩҮВ В ЩҲШӘШұШӘЫҢШЁ ШіШ§Щ„ЩҮШ§ЫҢ 29ШіШ§Щ„ЩҮ ЩҲ33ШіШ§Щ„ЩҮ В |
В В В В В Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢВ В В В В Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ В Ш§ШІ1ШӘШ§1440 |
ШіШ§Щ„ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Ш§ШІВ В Щ…ШЁШҜШ§В Ш¬Щ„Ш§Щ„ЫҢ |
Ъ©ШЁЫҢШіЩҮ ЩҮШ§ ЩҲШӘШұШӘЫҢШЁ ШіШ§Щ„ЩҮШ§ЫҢ 29ШіШ§Щ„ЩҮ ЩҲ33ШіШ§Щ„ЩҮ |
Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ Ш§ШІ1ШӘШ§1440 В |
ШіШ§Щ„ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Ш§ШІВ В Щ…ШЁШҜШ§В Ш¬Щ„Ш§Щ„ЫҢ |
Ъ©ШЁЫҢШіЩҮВ ЩҲ ШӘШұШӘЫҢШЁ ШіШ§Щ„ЩҮШ§ЫҢ 29ШіШ§Щ„ЩҮ ЩҲ33ШіШ§Щ„ЩҮ В |
Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢВ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ Ш§ШІ1ШӘШ§1440 |
В ШіШ§Щ„ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Ш§ШІВ Щ…ШЁШҜШ§В Ш¬Щ„Ш§Щ„ЫҢ |
||
|
0 |
0 |
458 |
29 |
520 |
978 |
29 |
1011 |
1473 |
||
|
29 |
29 |
487 |
33 |
553 |
1011 |
33 |
1044 |
1506 |
||
|
33 |
62 |
520 |
33 |
586 |
1044 |
33 |
1077 |
1539 |
||
|
33 |
95 |
553 |
33 |
619 |
1077 |
33 |
1110 |
1572 |
||
|
33 |
128 |
586 |
33 |
652 |
1110 |
33 |
1143 |
1605 |
||
|
33 |
161 |
619 |
33 |
685 |
1143 |
33 |
1176 |
1638 |
||
|
33 |
194 |
652 |
33 |
718 |
1176 |
33 |
1209 |
1671 |
||
|
33 |
227 |
685 |
33 |
751 |
1209 |
33 |
1242 |
1704 |
||
|
33 |
260 |
718 |
33 |
784 |
1242 |
33 |
1275 |
1737 |
||
|
33 |
293 |
751 |
33 |
817 |
1275 |
33 |
1308 |
1770 |
||
|
33 |
326 |
784 |
33 |
850 |
1308 |
33 |
1341 |
1803 |
||
|
33 |
359 |
817 |
33 |
883 |
1347 |
33 |
1374 |
1836 |
||
|
33 |
392 |
850 |
33 |
916 |
1374 |
33 |
1407 |
1869 |
||
|
33 |
425 |
883 |
33 |
949 |
1411 |
33 |
1440 |
1902 |
||
|
33 |
458 |
916 |
33 |
982 |
1444 |
***** |
****** |
*** |
||
|
33 |
491 |
949 |
*** |
****** |
*** |
***** |
****** |
*** |
||
В
В
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮВ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЫҢ ЩҶЫҢШіШӘ Ъ©ЩҮ ШЁШӘЩҲШ§ЩҶ ШЁШҜШ§ЩҶ Ш§Ш№ШӘЩ…Ш§ШҜ Ъ©ШұШҜ ЫҢШ§ ШЁШұШ§ШіШ§Ші ШўЩҶ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ЩҫШұШҜШ§Ш®ШӘ. ЩҲЩ„ЫҢ ЩҶЪ©ШӘЩҮ Щ…ЩҮЩ… ШҜШұ Ш§ЫҢЩҶ ШұЩҲШ§ЫҢШӘ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ (ЩӮШ§Ш¶ЫҢ ШІШ§ШҜЩҮ) Ш§ЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ Ш§ШІВ ШіШ§Щ„ 458 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШӘШ§ ШіШ§Щ„ 1275ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШҜЩӮЫҢЩӮШ§ ШҜШұ" Ш¬ШҜЩҲЩ„ ШӘШ·ШЁЫҢЩӮЫҢ ШіШ§Щ„ ЩҮШ§ЫҢВ Ъ©ШЁЫҢШіЩҮ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ" ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ ЩҲ ШЁШ§ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…Ш·Ш§ШЁЩӮШӘ ШҜШ§ШұШҜ ЩҲЩ„ЫҢ ШЁШ№ШҜ Ш§ШІ ШўЩҶ ШӘШ§ ЩҫШ§ЫҢШ§ЩҶ ШЁШ§ ЫҢЪ© ШіШ§Щ„ Ш§Ш®ШӘЩ„Ш§ЩҒ ШұЩҲШЁШұЩҲ Щ…ЫҢвҖҢШҙЩҲЫҢЩ…. ЫҢШ№ЩҶЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ ШіШ§Щ„вҖҢЩҮШ§ ШіШ§Щ„ ШЁШ№ШҜ Ш§ШІ ШўЩҶ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҮ Ш§ШіШӘШҢ Ъ©ЩҮ Щ…ЩҮЩ… ШӘШұ Ш§ШІ ЩҮЩ…ЩҮ ШіШ§Щ„ 1308 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ ШӘЩҶШёЫҢЩ…ЫҢ ЩӮШ§Ш¶ЫҢ ШІШ§ШҜЩҮ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ШЁЩҮ Ш®Ш§Ш·Шұ ЩҮЩ…ЫҢЩҶ ЫҢЪ© ШіШ§Щ„ Ш§Ш®ШӘЩ„Ш§ЩҒ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ШўЩ…ШҜЩҮ Ш§ШіШӘШҢ ШҜШұ ШөЩҲШұШӘЫҢ Ъ©ЩҮ ШЁШ§ЫҢШҜ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ ШіШ§Щ„ 1309 Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ Ъ©ЩҮВ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ш§ШіШӘ. ЩҲЩ„ЫҢ ШЁШ§ Ш§ЫҢЩҶ ЩҲШ¬ЩҲШҜ ЪҶЩҮШ§Шұ ШіШ§Щ„ 1176ШҢ1209ШҢ1242ЩҲ1275ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ЩҮШұ ЪҶЩҮШ§Шұ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮвҖҢШ§ЩҶШҜШҢ Ъ©ЩҮ Ш№Щ„Ш§ЩҲЩҮ ШЁШұ ШӘШ·ШЁЫҢЩӮ ШЁШ§ Ш¬ШҜЩҲЩ„ ШӘШ·ШЁЫҢЩӮЫҢ ЩҒЩҲЩӮвҖҢШ§Щ„Ш°Ъ©Шұ Ш§ЫҢЩҶ ЪҶЩҮШ§Шұ ШіШ§Щ„ ШҜШұ ШөЩҲШұШӘ ШӘШ·ШЁЫҢЩӮ Ш§ШІ ЩҶШёШұ Ш¬Ш§ЫҢЪҜШ§ЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЩҶЫҢШІ ШҜШұШіШӘ ШҜШұ Ш¬Ш§ЫҢЪҜШ§ЩҮ ЩҲШ§ЩӮШ№ЫҢ Ш®ЩҲШҜ ЩӮШұШ§Шұ ЪҜШұЩҒШӘЩҮвҖҢШ§ЩҶШҜ Ъ©ЩҮ ШЁЩҮ ШӘШұШӘЫҢШЁ Ш№ШЁШ§ШұШӘЩҶШҜ Ш§ШІ Ш®Ш§ЩҶЩҮвҖҢЩҮШ§ЫҢ 29ШҢ62ШҢ95 ЩҲ 128ШҢ Ъ©ЩҮ ШҜШұ ШўЩҶ ШіШ§Щ„ 1275 ШҜШұ Ш®Ш§ЩҶЩҮ 128 ЩҲ ЩӮШұШ§Шұ ШҜШ§ШұШҜ Ъ©ЩҮ ШіШ§Щ„ ЩҫШ§ЫҢШ§ЩҶЫҢ ЫҢЪ© ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҲ Ъ©ШЁЫҢШіЩҮ ШЁШ№ШҜЫҢ ШўЩҶ Ъ©ЩҮ ЫҢЪ© Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„ 1280 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲ ШҜ. ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ ШЁШ§Щ„Ш§ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜШҢ ЪҜШұЪҶЩҮ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШІЫҢШұ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 29ЩҲ33 ШіШ§Щ„ЩҮ Ш§Ш№ШӘЩӮШ§ШҜ ШҜШ§ШұШҜ ЩҲЩ„ЫҢ ЩӮШ§ШҜШұ ШЁЩҮ Ш§Ш¬ШұШ§ЫҢ ШөШӯЫҢШӯ ШўЩҶ ЩҶЫҢШіШӘ.
В ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШҜШұШіШӘ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ ЩҶШ®ШіШӘ ШЁШ§ЫҢШҜ Щ…ШЁШҜШ§ ШҜШұШіШӘЫҢ ШҜШұ Ш§Ш®ШӘЫҢШ§Шұ ШҜШ§ШҙШӘ. ЪҶШұШ§ Ъ©ЩҮ ШӘЩҶЩҮШ§ ШҜШұ ШөЩҲШұШӘ ШҜШұ Ш§Ш®ШӘЫҢШ§Шұ ШҜШ§ШҙШӘЩҶ ЫҢЪ© Щ…ШЁШҜШ§ ШҜШұШіШӘ ЩҲ ШҜЩӮЫҢЩӮ Ш§ШіШӘ Ъ©ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШҜШұШіШӘ ЩҫШұШҜШ§Ш®ШӘ. ЫҢШ№ЩҶЫҢВ ШЁШ§ ШҜШұ ШҜШіШӘ ШҜШ§ШҙШӘЩҶ ЫҢЪ© Щ…ШЁШҜШ§ ШҜШұШіШӘ ЩҲ ШҜЩӮЫҢЩӮ ЩҲ Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ Щ…ШЁШҜШ§ Ш¬ШҜЫҢШҜ ШЁЩҮ ЩҮЩ…Ш§ЩҶ ЩҶШӘЫҢШ¬ЩҮвҖҢШ§ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШұШіЫҢШҜ Ъ©ЩҮ ШҜШұ Ъ©ШӘШ§ШЁвҖҢЩҮШ§ЫҢ ЩҶШ¬ЩҲЩ…ЫҢ ЩҲ ШӘЩӮЩҲЫҢЩ…ЫҢ ШўЩ…ШҜЩҮ Ш§ШіШӘ. ЩҲ Ш§ЫҢЩҶ Щ…ШЁШҜШ§ ШҜШұШіШӘ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ШҜШұ Ъ©ШӘШ§ШЁ В«ШІШұШҜШҙШӘ ЩҲ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢВ» Щ…ЩҲШұШҜ ШЁШұШұШіЫҢ ЩӮШұШ§Шұ ЪҜШұЩҒШӘЩҮ ЩҮЩ…Ш§ЩҶШ§ Щ…ШЁШҜШ§ (Ш§ЫҢШұШ§ЩҶЫҢ -ШўШұЫҢШ§ЫҢЫҢ) Ш§ШіШӘ Ъ©ЩҮ 1128 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ЩҲ 507 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ Щ…ЫҢЩ„Ш§ШҜ Щ…ШіЫҢШӯ Ш§ШіШӘ.
Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ШЁШұШ§ЫҢ Щ…ШӯШ§ШіШЁЩҮШҢ ЩҶШ®ШіШӘ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1304 ЩҲ 1309 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШұШ§ ШЁШ§ Ш§ЩҒШІЩҲШҜЩҶ 1128 ШіШ§Щ„ ШЁЩҮ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ ШЁШҜЩ„ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… ЩҲ ШЁШ№ШҜ ШЁШұ Ш§ШіШ§Ші ЩҒШұЩ…ЩҲЩ„ ШЁШ§Щ„Ш§ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ Щ…ЫҢвҖҢЩҫШұШҜШ§ШІЫҢЩ… Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2432 = 1304 + 1128
888269=2422 /365Г—2432
2431 = 1303 + 1128
887903=2422 /365Г—2431
366=887903 вҖ“ 888269
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ш·ЩҲЩ„ ШіШ§Щ„ 1304ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2432 Ш§ЫҢШұШ§ЩҶЫҢ) 366 ШұЩҲШІ ШӘЩ…Ш§Щ… Ш§ШіШӘ ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Ш§ЫҢЩҶ ШіШ§Щ„ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ.
ШӯШ§Щ„ ЩҮЩ…ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШұШ§ ШЁШұШ§ЫҢ ШіШ§Щ„ 1309 Ш§ЩҶШ¬Ш§Щ… Щ…ЫҢ ШҜЩҮЫҢЩ…ШҢ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2437=1128+1309
890095=2422 /365Г—2437
2436=1128+1308
889729=2422 /365Г—2436
366 = 889729 - 890095
ЫҢШ№ЩҶЫҢ Ш·ЩҲЩ„ ШіШ§Щ„ 1309ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2437 Ш§ЫҢШұШ§ЩҶЫҢ) 366 ШұЩҲШІ ШӘЩ…Ш§Щ… Ш§ШіШӘ ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШіШ§Щ„ Щ…Ш°Ъ©ЩҲШұ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ .
В В В ЩҲЩ„ЫҢ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ЪҜЩҒШӘЩҮ ШҙШҜ ЪҜШұЩҲЩҮЫҢ Ш§ШІ ШӘЩӮЩҲЫҢЩ… ЩҶЪҜШ§ШұШ§ЩҶ Щ…Ш№Ш§ШөШұ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ЩҫЫҢШҙЩҶЩҮШ§ШҜ ШіЫҢШҜ ШӯШіЩҶ ШӘЩӮЫҢ ШІШ§ШҜЩҮ ШұШ§ ШҜШұ Щ…ЩҲШұШҜ 31 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш·ЩҲЩ„ 128 ШіШ§Щ„ ШұШ§ ШЁШіЫҢШ§Шұ Ш¬ШҜЫҢ ЪҜЩҒШӘЩҮ ЩҲ ШӘЩҶЩҮШ§ ШЁЩҮ Ш§ШӘЪ©Ш§ЫҢ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ШЁЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ Щ…ЫҢвҖҢЩҫШұШҜШ§ШІЩҶШҜШҢ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ Щ…ЫҢШ§ЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ Ш§ШІ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІШҢ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© ЩҲ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ЩҶШ§Щ… ШЁШұШҜ Ъ©ЩҮ ЩҶЩ…ЩҲЩҶЩҮ Ъ©Ш§Щ…Щ„ Ш§ЫҢЩҶ ЩҶЩҲШ№ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШұШ§ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҫЩҶШ¬ ЩҮШІШ§Шұ ШіШ§Щ„ЩҮ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШҜЫҢШҜ . ЩҮЩ…ЪҶЩҶЫҢЩҶ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ЩҲ ШЁЩҲЫҢЪҳЩҮ Щ…ШӯШ§ШіШЁШ§ШӘ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШҜШұ Ъ©ШӘШ§ШЁ В«ШІЫҢШ¬ Щ…Щ„Ъ©В» ЩҶЫҢШІЪ©ЩҮ ШҜШұШіШӘ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҲ ШЁЩҮ Ш®Ш§Ш·Шұ ЩҮЩ…ЫҢЩҶ ЩҮЩ… ШҜШ§ШұШ§ЫҢ Ш§ШҙШӘШЁШ§ЩҮ Ш§ШіШӘ. Ъ©ЩҮ Ш§ШІ ШЁЫҢЩҶ Ш§ЫҢЩҶ Ш§ШҙШӘШЁШ§ЩҮвҖҢЩҮШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ШӯШіШ§ШЁ Ъ©ШұШҜЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1276ШҢ1243 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜШұ ШөЩҒШӯЩҮвҖҢЩҮШ§ЫҢ 51 ЩҲ 52 Ъ©ШӘШ§ШЁ Ш§ШҙШ§ШұЩҮ Ъ©ШұШҜ Ъ©ЩҮ ШЁШұШ§ШіШ§Ші Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ…ЫҢ ШӘЩҮЫҢЩҮ ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ Ш§ШІ ШіШ§Щ„ 1220 ШӘШ§ 1368 ШӘЩҲШіШ· ШўЩӮШ§ЫҢШ§ЩҶ Ш§ШӯЩ…ШҜ ЩҶШ¬Щ… ШўШЁШ§ШҜЫҢШҢ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІШҢ ШӯШіШ§Щ… ШіШұЩ„ШӘЫҢШҢ ЩҲ Ш®ЩҲШҜ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШӘЩҮЫҢЩҮ ШҙШҜЩҮ Ш§ШіШӘ ЩҲ Ш§ЫҢШҙШ§ЩҶ Щ…Ш¬ШҜШҜШ§ ШҜШұ ШөЩҒШӯЩҮ 120 Ъ©ШӘШ§ШЁШҙШҢ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ Ш§ЫҢЩҶ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… ШұШ§ ШЁШ§ ШӘШ·ШЁЫҢЩӮ ШЁШ§ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 128 ШіШ§Щ„ЩҮ ШЁЩҮ ШөЩҲШұШӘ Ш¬ШҜЩҲЩ„ЫҢ ШӘЩҶШёЫҢЩ… Ъ©ШұШҜЩҮ Ш§ШіШӘШҢ Ъ©ЩҮ ШӘШ§ ШіШ§Щ„ 1366 Ш§ШҜШ§Щ…ЩҮ ШҜШ§ШұШҜ ЩҲ Ш¬Ш§ЫҢ ШіШ§Щ„ 1371 ШҜШұ ШўЩҶ ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ш®Ш§Щ„ЫҢ ЪҜШ°Ш§ШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ. ЩҲЩ„ЫҢ ШЁЩ„Ш§ЩҒШ§ШөЩ„ЩҮ ШҜШұ ШөЩҒШӯЩҮ ШЁШ№ШҜ Ъ©ШӘШ§ШЁ ШіШ§Щ„ 1371 ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Щ…Ш№ШұЩҒЫҢ ШҙШҜЩҮ Ш§ШіШӘ. ШўЩҶ ЩҮЩ… ШЁШ§ Ш§ЫҢШұШ§ШҜЫҢ ШЁШұ ШӘЩӮЩҲЫҢЩ… ШӘЩҶШёЫҢЩ…ЫҢ Щ…ШұЪ©ШІ ШӘЩӮЩҲЫҢЩ… (Щ…ЩҲШіШіЩҮ ЪҳЫҢЩҲЩҒЫҢШұЫҢЪ©) ШЁШұШ§ЫҢ ШіШ§Щ„вҖҢЩҮШ§ЫҢ ШЁЫҢЩҶ 1368 ШӘШ§ 1379ШҢ ЩҲ ШЁЩҮ Щ…ЩҲШ¶ЩҲШ№ Ъ©ШЁЫҢШіЩҮ ШҙЩ…ШұШҜЩҶ ШіШ§Щ„ 1370 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШӘЩҲШіШ· Щ…ЩҲШіШіЩҮ ШІШҰЩҲЩҒЫҢШІЫҢЪ© Ш§Ш№ШӘШұШ§Ш¶ ЩҲ ШЁЩҮ Ш§ШіШӘЩҶШ§ШҜ Ш¬ШҜЩҲЩ„ ШӘЩҶШ·ЫҢЩ…ЫҢ Ш®ЩҲШҜ (Ъ©ЩҮ ШЁШұ Ш§ШіШ§Ші ШҜЩҲШұЩҮ Ш«Ш§ШЁШӘ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШӘЩҶШ·ЫҢЩ… ШҙШҜЩҮ Ш§ШіШӘ) ШіШ§Щ„ 1371 ШұШ§ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Щ…ЫҢвҖҢШҜШ§ЩҶШҜ ЩҶЩҮ ШіШ§Щ„ 1370 ШұШ§.
ЩҲ Ш§ЫҢЩҶ ЩҶЫҢШіШӘ Щ…ЪҜШұ ШЁЩҮ Ш®Ш§Ш·Шұ ЩӮШ·Ш№ЫҢ ЩҲ Ш«Ш§ШЁШӘ ЪҜШұЩҒШӘЩҶ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 128 ШіШ§Щ„ЩҮШҢ ЩҲ ЩҶШ§ШҜЫҢШҜЩҮ ЪҜШұЩҒШӘЩҶ ШұЩӮЩ… 0016/0ШұЩҲШІЫҢ ШҜШұ ЩҮЩҶЪҜШ§Щ… Щ…ШӯШ§ШіШЁЩҮ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Щ…ЩҲШ¬ЩҲШҜ ШҜШұ ЩҮШұ 128 ШіШ§Щ„ ЩҲ ШЁШіЩҶШҜЩҮ Ъ©ШұШҜЩҶ ШЁЩҮ 31 ШұЩҲШІ ЫҢШ§ 31 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШӘЩ…Ш§Щ… ШҜШұ ЩҮШұ 128 ШіШ§Щ„ Ш§ШІ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ. ШҜШұ ШөЩҲШұШӘЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ ШұЩӮЩ… ШЁЩҮ ШёШ§ЩҮШұ Ш¬ШІЫҢЫҢ 0016/0 ШұЩҲШІЫҢ ( Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ ШӘШЁШҜЫҢЩ„ ШЁЩҮ Ш«Ш§ЩҶЫҢЩҮ Ш№ШЁШ§ШұШӘ Ш§ШІ 138 Ш«Ш§ЩҶЫҢЩҮ Щ…ЫҢ ШҙЩҲШҜ) ШЁШ§ ЪҜШ°ШҙШӘ ШіШ§Щ„вҖҢЩҮШ§ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШЁЩҮ ШӯШҜЫҢ Щ…ЫҢвҖҢШұШіШҜ Ъ©ЩҮ ШҜШұ ШӘШ№ЫҢЫҢЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШӘШ§Ш«ЫҢШұ ЪҜШ°Ш§Шұ ШЁШ§ШҙШҜ.
Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜЫҢШҜ Ъ©ЩҮ ШҜШұ ЩҮШұ 673 ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢШҢ Ш§ЫҢЩҶ Ш§Ш®ШӘЩ„Ш§ЩҒ Ш¬ШІЫҢЫҢ ШЁЩҮ ЫҢЪ© ШұЩҲШІ Ш§Ш®ШӘЩ„Ш§ЩҒ ШҜШұ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШӘШЁШҜЫҢЩ„ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ ЫҢШ№ЩҶЫҢ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШіШ§Щ„ 674 Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ШіШ§Щ„ 673 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ:
245808=2422 /365Г—673
245442=2422 /365Г—672
366= 245442 - 245808
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ ШіШ§Щ„ 673 ЫҢЪ© ШіШ§Щ„ 366 ШұЩҲШІЩҮ ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ. ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШҜШұЫҢШ§ЩҒШӘ Ъ©ЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШЁШ§ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ ШҜШұШіШӘ ЩҶЫҢШіШӘ ЩҲ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЫҢ Ъ©ЩҮ Щ…ЫҢвҖҢШЁЫҢЩҶЫҢЩ… ШҜШұ ЩҮШұ 673 ШіШ§Щ„ ЫҢЪ© ШіШ§Щ„ Ш§ШҙШӘШЁШ§ЩҮ Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҙШӘ.
Ш§ШІ ШіЩҲЫҢ ШҜЫҢЪҜШұ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ 673 ШіШ§Щ„ЩҮ ШЁЩҮ ШҜЩ„ЫҢЩ„ Ъ©ШіШұЫҢ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Ш§ЩҶШҜЪ©ЫҢ Ъ©ЩҮ ШҜШ§ШұШҜ Ш§ШІ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Ъ©Ш§Щ…Щ„вҖҢШӘШұ Ш§ШіШӘ. ЪҶШұШ§ Ъ©ЩҮ ШҜШұЩҮШұ 128 ШіШ§Щ„ ШҜШ§ШұШ§ЫҢ 31 ШұЩҲШІ Ъ©ШЁЫҢШіЩҮ ШЁШ№Щ„Ш§ЩҲЩҮ 0016/0 ШұЩҲШІ ЫҢШ§ 138 Ш«Ш§ЩҶЫҢЩҮ Ъ©ШіШұЫҢ Ш§Ш¶Ш§ЩҒЫҢ ШҜШ§ШұЫҢЩ…ШҢ ЩҲЩ„ЫҢ ШҜШұ ЫҢЪ© ШҜЩҲШұЩҮ 673 ШіШ§Щ„ЩҮ Щ…ЫҢШІШ§ЩҶ Ш§ЫҢЩҶ Ъ©ШіШұЫҢ ШЁЩҮ 0006/0 ШұЩҲШІ ЫҢШ§ ШӯШҜЩҲШҜ 51 Ш«Ш§ЩҶЫҢЩҮ Щ…ЫҢвҖҢШұШіШҜ.
Ш§ШІ ШіЩҲЫҢ ШҜЫҢЪҜШұ ШҜЩҲШұЩҮ 673 ШіШ§Щ„ЩҮ ЪҶЫҢШІЫҢ ЩҶЫҢШіШӘ Ш¬ШІ ЩҫЩҶШ¬ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁШ№Щ„Ш§ЩҲЩҮ ЫҢЪ© ШІЫҢШұ ШҜЩҲШұЩҮ 33ШіШ§Щ„ЩҮ.
Ъ©ЩҮ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЫҢ ЫҢШ§ШҜШўЩҲШұ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 161 ШіШ§Щ„ЩҮ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ Ш·ЩҲШіЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШўЩҶ 161 ШіШ§Щ„ ЪҶЫҢШІЫҢ ЩҶЫҢШіШӘ Щ…ЪҜШұ ЫҢЪ© ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁШ№Щ„Ш§ЩҲЩҮ ЫҢЪ© ШІЫҢШұ ШҜЩҲШұЩҮ 33ШіШ§Щ„ЩҮ.
Ш§Щ„ШЁШӘЩҮ ШЁШ§ Ш§ЫҢЩҶ ШӘЩҲШ¬ЩҮ Ъ©ЩҮ Ш®ЩҲШҜ 33ШіШ§Щ„ ШЁЩҮ ШӘЩҶЩҮШ§ЫҢЫҢ ЩҶЩӮШҙЫҢ ЩҶШҜШ§ШұШҜ ЩҲШӘЩҶЩҮШ§ ШҜШұ ШӘШұЪ©ЫҢШЁ ШЁШ§ 128 ШіШ§Щ„ (ШҜШұ ШҜЩҲШұЩҮ 161 ШіШ§Щ„ЩҮ Ш®ЩҲШ§Ш¬ЩҮ ЩҶШөЫҢШұШ§Щ„ШҜЫҢЩҶ ШӘЩҲШіЫҢ) ЩҲ ШҜШұ ШӘШұЪ©ЫҢШЁ ШЁШ§ 640 ШіШ§Щ„ ЫҢШ§ ЩҫЩҶШ¬ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШҜШұ Щ…ШӯШ§ШіШЁЩҮ Щ…Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШӘШ§Ш«ЫҢШұ ЪҜШ°Ш§Шұ Ш®ЩҲШ§ЩҮШҜ ШҙШҜШҢ ШўЩҶ ЩҮЩ… ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· 2422/365 ШұЩҲШІ .
ЩҲ ШЁШұШҜШ§ШҙШӘ ШЁШұШ®ЫҢ Ъ©ЩҮ ЪҜЩ…Ш§ЩҶ Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ Ш®ЩҲШҜ 33 ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ ШЁШұШҜШ§ШҙШӘЫҢ Ш§ШіШӘ ЩҶШ§ШҜШұШіШӘ. Ш§ЫҢЩҶ ШІЫҢШұ ШҜЩҲШұЩҮ 33 ШіШ§Щ„ЩҮ ШҜШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш§Щ…ШұЩҲШІЫҢ Ъ©ЩҮ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ ШұШ§ 2422/365 ШұЩҲШІ Щ…ЫҢвҖҢШҙЩ…Ш§ШұЩҶШҜ ШЁЩҮ ШӘЩҶЩҮШ§ЫҢЫҢ ЩҮЫҢЪҶ ЩҶЩӮШҙ ШӘШ№ЫҢЫҢЩҶ Ъ©ЩҶЩҶШҜЩҮвҖҢШ§ЫҢ ЩҶШҜШ§ШұШҜ ЩҲ ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶШҜ ЩҮЩ… ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ШҜЩҲШұЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ Щ…ШӯШіЩҲШЁ ШҙЩҲШҜ. ШЁШұШ§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШҜШұ ЩҮШұ 33ШіШ§Щ„ ЩҮШҙШӘ ШіШ§Щ„ ШӘЩ…Ш§Щ… Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ШЁШ§ЫҢШҜ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ Ш®ЩҲШұШҙЫҢШҜЫҢ 242424/365 ШұЩҲШІ ШЁШ§ШҙШҜШҢ Ъ©ЩҮ ЪҶЩҶЫҢЩҶ ЩҶЫҢШіШӘ ЩҲ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ЩҮЩ… ЪҶЩҶЫҢЩҶ ЩҶШЁЩҲШҜЩҮ Ш§ШіШӘ. ШЁШұШ§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· 242424/365 ШұЩҲШІ ШҜЫҢЪҜШұ Щ…ШӯЩ„ЫҢ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЩҲ ЫҢШ§ 161 ШіШ§Щ„ЩҮ ЩҲ ШӯШӘЫҢ 673 ШіШ§Щ„ЩҮ ШЁШ§ЩӮЫҢ ЩҶЩ…ЫҢвҖҢЩ…Ш§ЩҶШҜШҢ ЩҲ ШӘЩҶЩҮШ§ Ш¬ШҜЩҲЩ„вҖҢЩҮШ§ ЩҲ ШІЫҢШ¬вҖҢЩҮШ§ЫҢ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Ш§ШІ Щ…ЩҶШ¬Щ…Ш§ЩҶ ЩҫЫҢШҙЫҢЩҶ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ ШӘШ§ ЩҶШ§ШҜШұШіШӘ ШЁЩҲШҜЩҶ ЪҶЩҶЫҢЩҶ ЩҒШұШ¶ЫҢЩҮвҖҢШ§ЫҢ ШұШ§В Ш«Ш§ШЁШӘ Ъ©ЩҶШҜ.
ШЁЩҮ ЩҮШұ ШӯШ§Щ„ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ЪҜЩҒШӘЩҮ ШҙШҜ ШЁЩҮ Ш®Ш§Ш·Шұ ЩӮШ·Ш№ЫҢ ЩҲ Ш«Ш§ШЁШӘ ЩҒШұШ¶ Ъ©ШұШҜЩҶ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҮЩ… ШҜШұ ШӘШ·ШЁЫҢЩӮ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Щ…ШөЩҲШЁ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШЁШ§ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ 128 ШіШ§Щ„ЩҮ ЩҲ ЩҶЫҢШІ ШӘШ№ЫҢЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ЩҲШ§ЩӮШ№ЫҢ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (Ъ©ЩҮ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ШЁЩҲШҜЩҮ Ш§ШіШӘ ) ЩҲ ЩҶЫҢШІ ШіШ§Щ„ 1309 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (Ъ©ЩҮ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЩҲШҜЩҮ Ш§ШіШӘ) ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЩҲ ШЁЩҮ ШӘШЁШ№ ШўЩҶ Ъ©ШЁЫҢШіЩҮ ЪҜШұЩҒШӘЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1276 ЩҲ 1371 ШЁЩҮ Ш¬Ш§ЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ 1275 ЩҲ 1370ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§ЩӮШҜШ§Щ… Ъ©ШұШҜЩҮвҖҢШ§ЩҶШҜ. Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШЁШұШұШіЫҢ Ш§ЫҢЩҶ ШҜЩҲ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ Щ…ЫҢвҖҢЩҫШұШҜШ§ШІЫҢЩ…:
Ш§ЩҲЩ„ ШЁЩҮ ШЁШұШұШіЫҢ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ЫҢШ§ ЩҶШЁЩҲШҜЩҶ ШіШ§Щ„ 1371 Щ…ЫҢ ЩҫШұШҜШ§ШІЫҢЩ…ШҢЪ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2499=1128 +1371
2498=1128 +1370
912740=2422 /365Г—2499
912375=2422 /365Г—2498
365 = 912375 - 912740
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШіШ§Щ„ 1371 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…Ш·Ш§ШЁЩӮ ШЁШ§ 2499 Ш§ЫҢШұШ§ЩҶЫҢШҢ ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш§ШіШӘ ЩҶЩҮ Ъ©ШЁЫҢШіЩҮ .
ШӯШ§Щ„ Ш§ЪҜШұ Ш§ЫҢЩҶ ШўШІЩ…Ш§ЫҢШҙ ШұШ§ ШЁШ§ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ Ш§ШҜШ§Щ…ЩҮ ШЁШҜЩҮЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
480 +(673Г—3) = 673Г·2499
96 +(128Г—3) =128Г· 480
Ъ©ЩҮ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШұЩӮЩ… 96ШҢ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Ш§ЫҢЩҶ Ш№Щ…Щ„ЫҢШ§ШӘШҢ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШұШҜ ШЁШ§ШІ Щ…Ш№Щ„ЩҲЩ… Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ ШіШ§Щ„ 2499 Ш§ЫҢШұШ§ЩҶЫҢ ЫҢШ§ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„ 1371 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш§ШіШӘ ЩҶЩҮ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ.
ШӯШ§Щ„ ШЁШұШ§ЫҢ ШўШІЩ…Ш§ЫҢШҙ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ЫҢШ§ ЩҶШЁЩҲШҜЩҶ ШіШ§Щ„ 1276ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (2404 Ш§ЫҢШұШ§ЩҶЫҢ) ШЁЩҮ ШӘШұШӘЫҢШЁ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2404 =1128 +1276
2403= 1128+1275
878042= 2422 /365Г—2404
877677=2422 /365Г—2403
365 =877677 - 878042
ШҜШұ ЩҶШӘЫҢШ¬ЩҮ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ Щ…Ш№Щ„ЩҲЩ… Щ…ЫҢвҖҢШҙЩҲШҜ ШіШ§Щ„ 1276ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ(2404Ш§ЫҢШұШ§ЩҶЫҢ) ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш§ШіШӘ ШҢ ЩҶЩҮ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ.ЩҮЩ…ЫҢЩҶ Ш·ЩҲШұ ШҜШұ ШөЩҲШұШӘ ШўШІЩ…Ш§ЫҢШҙ ШЁШ§ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ШҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
385 + (673Г—3 ) =673Г·2404
1 + (128Г—3 ) =128 Г·385
Ъ©ЩҮ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ ЩҲШ¬ЩҲШҜ ЩҶШҜШ§ШұШҜ Щ…Ш№Щ„ЩҲЩ… Щ…ЫҢвҖҢЪҜШұШҜШҜ Ъ©ЩҮ ШіШ§Щ„ 1276ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (2404 Ш§ЫҢШұШ§ЩҶЫҢ) ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш§ШіШӘ ЩҶЩҮ Ъ©ШЁЫҢШіЩҮ.
ЩҲ ШҜШұ ЩҶШӘЫҢШ¬ЩҮ Щ…ШҙШ®Шө Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ Ш§ШёЩҮШ§ШұШ§ШӘ ШўЩӮШ§ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШЁЩҲЫҢЪҳЩҮ ШҜШұ Щ…ЩҲШұШҜ ШіШ§Щ„ 1371ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШҜЩӮЫҢЩӮШ§ Ш§ШҙШӘШЁШ§ЩҮ ЩҲ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ. ЩҲ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ Ш·ШЁЩӮ ШӘЩӮЩҲЫҢЩ… Ш¬Ш§ШұЫҢ ШіШ§Щ„ 1370 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁШ§Щ„Ш§ ШіШ§Щ„ 1370ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ. Ш§ЩҒШІЩҲЩҶ ШЁШұШ§ЫҢЩҶ Ъ©ЩҮ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҫЩҶШ¬ ЩҮШІШ§Шұ ШіШ§Щ„ЩҮ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© ЩҮЩ… ШіШ§Щ„ 1370 ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁЩҮ ШҙЩ…Ш§Шұ ШўЩ…ШҜЩҮ Ш§ШіШӘ.
ЩҲ Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© ЩҮЩ…Ш§ЩҶ Щ…ШЁШҜШ§ 2346 ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ Ш§ШіШӘШҢ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШөШӯШӘ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„ 1370 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҫЩҶШ¬ ЩҮШІШ§Шұ ШіШ§Щ„ЩҮ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© ШұШ§ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· 2422/365 ШұЩҲШІ ЩҲ ЩҶЫҢШІ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673ШіШ§Щ„ЩҮ ЩҲ128 ШіШ§Щ„ЩҮ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜШҢ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
3716 = 2346 +1370
3715 =2346 +1369
1357240 = 2422 /365Г—3716
1356874 =2422 /365Г— 3715
366 = 1356874 0- -1357240
351 + ( 673Г—5 ) = 673 Г· 3716
95 + ( 128 Г—2 ) = 128 Г· 351
Ъ©ЩҮ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ЩҶШӘЫҢШ¬ЩҮ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁШ§ШӘ ЩҲ Ш·ЩҲЩ„ ШіШ§Щ„ 366 ШұЩҲШІ ШЁШұШ§ЫҢ ШіШ§Щ„ 1370 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (3716ШЁЩҮШұЩҲШІ ЩҲ ШЁЫҢШұШҙЪ©)ЩҲ ЩҶЫҢШІ Ш®Ш§ЩҶЩҮ 95 ШЁЩҮ ШҜШіШӘ ШўЩ…ШҜЩҮ ШЁШұШ§ЫҢ ЩҮЩ…ЫҢЩҶ ШіШ§Щ„ Щ…ШҙШ®Шө Ш§ШіШӘ Ъ©ЩҮ Щ…ШӯШ§ШіШЁЩҮ Щ…Ш§ ЩҲ ШЁЩҮШұЩҲШІ ЩҲ ШЁЫҢШұШҙЪ© ШҜШұШіШӘ Ш§ШіШӘ ЩҲ Щ…ШӯШ§ШіШЁЩҮ ШұШӯЫҢЩ… ШұШ¶Ш§ШІШ§ШҜЩҮ Щ…Щ„Ъ© ЩҶШ§ШҜШұШіШӘ.
ШӯШ§Щ„ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЩҶШЁЩҲШҜЩҶ ШіШ§Щ„ 1371 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШҜЩӮЫҢЩӮШ§ Щ…Ш№Щ„ЩҲЩ… Щ…ЫҢвҖҢШҙЩҲШҜ Ъ©ЩҮ Ш¬ШҜЩҲЩ„ ШӘЩҶШёЫҢЩ…ЫҢ ШұШӯЫҢЩ… ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШҜШұ Ъ©ШӘШ§ШЁ В«ШІЫҢШ¬ Щ…Щ„Ъ©В» ШЁШұШ§ЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ 1222ШӘШ§В 1366 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ ЩҶЫҢШІ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„ 1371 (Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁШ№ШҜ Ш§ШІ ШіШ§Щ„ 1366) ШҜШұ ШөЩҒШӯЩҮ 121 Ъ©ШӘШ§ШЁ ШЁШ§ЫҢШҜ ШЁЩҮ Ш§ШөЩ„Ш§Шӯ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ЩҫШұШҜШ§Ш®ШӘ ЩҲ ШЁЩҮ Ш№ШЁШ§ШұШӘ ШҜЫҢЪҜШұ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1275 ЩҲ 1370 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ЩҲ ЩҶЫҢШІ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1304 ЩҲ 1309 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШҜШұШіШӘ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1275 вҖ“ 1304 вҖ“ 1309 вҖ“ 1370 ШҜШұВ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШӘШ№ЫҢЫҢЩҶ Ъ©ШұШҜ.
Ш§Щ…Ш§ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШҜЫҢШҜЫҢЩ… (ШҜШұ Щ…ШӯШ§ШіШЁШ§ШӘ ШЁШ§Щ„Ш§) Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1275ШҜШұ Ш®Ш§ЩҶЩҮ
ШўШ®Шұ ЫҢШ§ Ш®Ш§ЩҶЩҮ ШіШ§Щ„ 128 Ш§ШіШӘ ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1370 ШҜШұ Ш®Ш§ЩҶЩҮ 95 Ш¬ШҜЩҲЩ„ШҢ ШӯШ§Щ„Ш§ ШЁШ§ ЩҮЩ…Ш§ЩҶ ШұЩҲШҙ ШЁЩҮ ШӘШ№ЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1304 ЩҲ 1309 ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ Щ…ЫҢвҖҢЩҫШұШҜШ§ШІЫҢЩ… Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2432 = 1128+ 1304
413 +( 673Г—3 )=673Г—2432
29+ (128Г—3 )=128Г· 413
2437 = 1128 +2437
418 +( 673Г—3 )=673 Г·2437
34 +( 128Г—3 )=128 Г·418
ШҜШұЩҶШӘЫҢШ¬ЩҮ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ ШҜШұ ШҜЩҲ ЩҒШұЩ…ЩҲЩ„ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ ШЁШ§Щ„Ш§ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜШҢ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ( 2432 Ш§ЫҢШұШ§ЩҶЫҢ) ШҜШұ Ш®Ш§ЩҶЩҮ ШҙЩ…Ш§ШұЩҮ 29 ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1309ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2437Ш§ЫҢШұШ§ЩҶЫҢ) ШҜШұ Ш®Ш§ЩҶЩҮ 34 Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЩӮШұШ§Шұ Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҙШӘ.
ШӯШ§Щ„Ш§ ШЁШ§ ШұЩҲШҙЩҶ ШҙШҜЩҶ ШіЩҮ ШіШ§Щ„ Ъ©Щ„ЫҢШҜЫҢ Ш§ШІ ЫҢЪ© ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ Ш§ЫҢЩҶ ШіШ§Щ„ ЩҮШ§ ШұШ§ ШҜШұ Ш¬ШҜЩҲЩ„ЫҢ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ ШЁЩҮ ЩҶЩ…Ш§ЫҢШҙ ЪҜШ°Ш§ШҙШӘШҢ Ъ©ЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ:
В
В
|
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|
В |
В |
В |
В |
В |
В |
В |
1275 |
|
В |
В |
В |
В |
В |
В |
1304 |
В |
|
1309 |
В |
В |
В |
В |
В |
В |
В |
|
В |
В |
В |
В |
В |
В |
В |
1370 |
|
В |
В |
В |
В |
В |
В |
В |
В |
В
В
Ъ©ЩҮ ШҜШұ ШўЩҶ ШіШ§Щ„ 1275 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2403Ш§ЫҢШұШ§ЩҶЫҢ) ЩҫШ§ЫҢШ§ЩҶ ЫҢЪ© ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҲ ШҜЩҲШұЩҮ Ш¬ШҜЫҢШҜ 128 ШіШ§Щ„ЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ ШЁШ№ШҜ Ш§ШІ ШўЩҶ ЫҢШ№ЩҶЫҢ Ш§ШІ ШіШ§Щ„ 1280 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2408Ш§ЫҢШұШ§ЩҶЫҢ) ШўШәШ§ШІ ЩҲ ШҜШұ ШіШ§Щ„ 1403ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (2531Ш§ЫҢШұШ§ЩҶЫҢ) ШЁЩҮ ЩҫШ§ЫҢШ§ЩҶ Щ…ЫҢвҖҢШұШіШҜ.
ЪҜЩҒШӘЩҶЫҢ Ш§ШіШӘ ЩӮШіЩ…ШӘ Ш№Щ…ШҜЩҮвҖҢШ§ЫҢ Ш§ШІ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… Щ…ЩҲШұШҜ Ш§ШіШӘЩҶШ§ШҜ ЩҲ Ш§ШіШӘЩҒШ§ШҜЩҮ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШҜШұ Ъ©ШӘШ§ШЁ ШІЫҢШ¬ Щ…Щ„Ъ© (ШөШө50 ЩҲ 51) ЫҢШ№ЩҶЫҢ ШӘЩӮЩҲЫҢЩ… ШіШ§Щ„ ЩҮШ§ЫҢ 1230 ШӘШ§ 1304 (ЫҢШ№ЩҶЫҢ ШіШ§Щ„вҖҢЩҮШ§ЫҢ ЩҫЫҢШҙ Ш§ШІ ШӘШөЩҲЫҢШЁ ЩӮШ§ЩҶЩҲЩҶ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜШұ ШіШ§Щ„ 1304) Ъ©Ш§ШұЫҢ Ш§ШіШӘ ШӘШ·ШЁЫҢЩӮЫҢ Ъ©ЩҮ ШӘЩҲШіШ· Ш§ШӯЩ…ШҜ ЩҶШ¬Щ… ШўШЁШ§ШҜЫҢ ШөЩҲШұШӘ ЪҜШұЩҒШӘЩҮ Ш§ШіШӘ ЩҲ Ш§ШҙШӘШЁШ§ЩҮ Щ…ШӯШ§ШіШЁЩҮ ШҜШұШўЩҶ ШӯШӘЩ…ЫҢ Ш§ШіШӘ ЪҶШұШ§ Ъ©ЩҮ ШҜШұ ШіШ§Щ„ ЩҮШ§ЫҢ 1230 ШӘШ§ 1304 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШӘЩӮЩҲЫҢЩ… Ш®ЩҲШұШҙЫҢШҜЫҢ ШЁЩҮ ШҙЫҢЩҲЩҮЩ” Ш§Щ…ШұЩҲШІЫҢ Щ…Ш№Щ…ЩҲЩ„ ЩҶШЁЩҲШҜЩҮ ШЁЩ„Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ ШәШ§ШІШ§ЩҶЫҢ Щ…Ш№Щ…ЩҲЩ„ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЩҲ ШӘШЁШҜЫҢЩ„ ШҜЩӮЫҢЩӮ ШўЩҶвҖҢЩҮШ§ ШЁЩҮ ЪҜШ§ЩҮШҙЩ…Ш§Шұ Ш®ЩҲШұШҙЫҢШҜЫҢ Ъ©Ш§Шұ ШіШ§ШҜЩҮвҖҢШ§ЫҢ ЩҶЫҢШіШӘ.
В ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ЩҮЩ… ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШҜШұЫҢШ§ЩҒШӘ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… Щ…ЩҲШұШҜ Ш§ШіШӘЩҶШ§ШҜ ШўЩӮШ§ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© Ш№Щ„Ш§ЩҲЩҮ ШЁШұ ШіШ§Щ„ ЩҮШ§ЫҢ 1276В ЩҲ 1371ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢШҢ ШіШ§Щ„ 1243ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШұШ§ ЩҶЫҢШІ ШЁЩҮ Ш§ШҙШӘШЁШ§ЩҮ Ъ©ШЁЫҢШіЩҮ ШҙЩ…ШұШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ШҜШұШіШӘ ЩҶЫҢШіШӘ ЩҲ ШҜШұ ШӯЩӮЫҢЩӮШӘ ШіШ§Щ„ 1242 Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ЩҶЩҮ ШіШ§Щ„ 1243. Ш¬Ш§Щ„ШЁ Ш§ЫҢЩҶШ¬Ш§ШіШӘ Ъ©ЩҮ ШўЩӮШ§ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШҜШұ ЩҮЩ…Ш§ЩҶ Ъ©ШӘШ§ШЁ ЩҒЩҲЩӮ Ш§Щ„Ш°Ъ©Шұ ШҜШұ ШөЩҒШӯЩҮвҖҢЩҮШ§ЫҢ 65 ШӘШ§ 68 ШЁЩҮ В«ШӘЩӮЩҲЫҢЩ… ЩҶЩҲШұЩҲШІЫҢ ШҙЩҮШұЫҢШ§ШұЫҢВ» Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ШҜШұ Щ…ЩҲШұШҜ Ъ©ШЁЫҢШіЩҮ ШҙЩ…ШұШҜЩҶ ШіШ§Щ„ 1242 Ш§Ш№ШӘШұШ§Ш¶ Щ…ЫҢвҖҢЪ©ЩҶШҜ ЩҲ Ш№Щ„ШӘ ШўЩҶ ШұШ§ ШЁШ§ШІ ШЁШ§ Щ…ШұШ§Ш¬Ш№ЩҮ ШЁЩҮ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… Ш§ШіШӘШ®ШұШ§Ш¬ЫҢ Ш§ШӯЩ…ШҜ ЩҶШ¬Щ… ШўШЁШ§ШҜЫҢ ЩҲШҜЫҢЪҜШұШ§ЩҶШҢ ШҜШұ Щ…ШәШ§ЫҢШұШӘ ШўЩҶ ШЁШ§ Щ…ШӘЩҶ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… Щ…Ш°Ъ©ЩҲШұ Щ…ЫҢвҖҢШҜШ§ЩҶШҜ Ъ©ЩҮ ШҜШұ ШўЩҶ ШЁЩҮ Ш¬Ш§ЫҢ ШіШ§Щ„ 1242 ШіШ§Щ„ 1243 Ъ©ШЁЫҢШіЩҮ ШҙЩ…ШұШҜЩҮ ШҙШҜЩҮ Ш§ШіШӘ.
ШӯШ§Щ„ ШЁШұ Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁШҜШ§ЩҶЫҢЩ… ШӯЩӮ ШЁШ§ Ъ©ЫҢШіШӘ Ъ©Ш§ЩҒЫҢ Ш§ШіШӘ ШіШ§Щ„ 1242ШұШ§ ШЁЩҮ ШұЩҲШҙ ШЁШ§Щ„Ш§ ЩҲ ШЁШ§ Ш§ЩҒШІЩҲШҜЩҶ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ Щ…ШӯШ§ШіШЁЩҮ Ъ©ЩҶЫҢЩ…ШҢ Ъ©ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
2370 = 1128В + 1242
865624 = 2422 /365Г— 2370
865258 =В 2422 /365 Г— 2369
366 = 865258 вҖ“ 865624
351 +( 673Г—3 )= 673 Г·2370
95 + ( 128Г— 2 ) = 128Г· 351
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ЪҶЩҲЩҶ Ш·ЩҲЩ„ ШіШ§Щ„ 1242ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (2370Ш§ЫҢШұШ§ЩҶЫҢ) ШҜЩӮЫҢЩӮШ§ 366 ШұЩҲШІ Ш§ШіШӘ ЩҫШі Ш§ЫҢЩҶ ШіШ§Щ„ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШўЩҶ ЩҮЩ… ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ ШҜШұ Ш®Ш§ЩҶЩҮ 95 Щ…ЫҢ ШЁШ§ШҙШҜ.
Щ„Ш§ШІЩ… ШЁЩҮ ЫҢШ§ШҜ ШўЩҲШұЫҢ ЩҶЫҢШіШӘ Ъ©ЩҮ Ш§ЫҢЩҶ Щ…ЩҲШ¶ЩҲШ№ ЫҢШ№ЩҶЫҢ Ъ©ЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1242ШҢ 1275 ЩҲ 1280 (ШЁЩҮ Ш№ЩҶЩҲШ§ЩҶ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ) ШұШ§ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШҜШұЩ…ЩҲШұШҜ ШӘШ·ШЁЫҢЩӮ Ш¬ШҜЩҲЩ„ 1440 ШіШ§Щ„ЩҮ ЩӮШ§Ш¶ЫҢ ШІШ§ШҜЩҮ Щ…ЫҢШұЩ… ЪҶЩ„ШЁЫҢ ШЁШ§ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Щ…ЩҲШұШҜ ШЁШұШұШіЫҢ ЩӮШұШ§Шұ ЪҜШұЩҒШӘ ЩҲ ШҜШұШіШӘЫҢ ШўЩҶ ЩҮШ§ Щ…ШӯШұШІ ЪҜШұШҜЫҢШҜ.
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ШЁЩҮ ШұЩҲШҙЩҶЫҢ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶШӘЫҢШ¬ЩҮ ЪҜШұЩҒШӘ Ъ©ЩҮ Щ…ШӯШ§ШіШЁЩҮ ШўЩӮШ§ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ЩҲ ЩҶЫҢШІ ШўЩҶЪҶЩҮ ШҜШұ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… ШўЩӮШ§ЫҢ Ш§ШӯЩ…ШҜ ЩҶШ¬Щ… ШўШЁШ§ШҜЫҢ ШўЩ…ШҜЩҮ ШәЩ„Ш· Ш§ШіШӘ.
Ъ©ЩҮ Ш№Щ„ШӘ Ш§ЫҢЩҶ Ш§ШҙШӘШЁШ§ЩҮ ЩҮШ§ ШҜШұ ШӯЩӮЫҢЩӮШӘ ШҜШұ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ ЩҲ ЩӮШ·Ш№ЫҢ ЩҫЩҶШҜШ§ШҙШӘЩҶ Щ…ЩҲШ¶ЩҲШ№ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ.
ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ЩҮЩ… Ш¬ШҜЩҲЩ„ ШөЩҒШӯЩҮ 120 Ъ©ШӘШ§ШЁ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ( Ш¬ШҜЩҲЩ„ ШӘЩҶШёЫҢЩ…ЫҢ ШЁШұШ§ЫҢ Ш®Щ„Ш§ШөЩҮ ШӘЩӮЩҲЫҢЩ… Ш§ШӯЩ…ШҜ ЩҶШ¬Щ… Ш§ШЁШ§ШҜЫҢ ЩҲ ШҜЫҢЪҜШұШ§ЩҶ) Ъ©ЩҮ ШЁШұШ§ШіШ§Ші ЩҮЩ…ЫҢЩҶ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ ШӘЩҶШёЫҢЩ… ШҙШҜЩҮ Ш§ШіШӘ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ. Ъ©ЩҮ ШЁШұШ§ЫҢ ШўШҙЩҶШ§ЫҢЫҢ ШЁШ§ ШўЩҶ Ш№ЫҢЩҶ Ш¬ШҜЩҲЩ„ Щ…Ш°Ъ©ЩҲШұ ШЁШ§ Ш§ЩҒШІШ§ЫҢШҙ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1362 ШӘШ§ 1383ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (ШЁШұ Ш§ШіШ§Ші ШӘЩҲШ¶ЫҢШӯШ§ШӘ Ш§ЫҢШҙШ§ЩҶ ШҜШұ ШөЩҒШӯЩҮ 121 Ъ©ШӘШ§ШЁ) ШұШ§ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ Щ…ЫҢ ШўЩҲШұЫҢЩ…:
Ш¬ШҜЩҲЩ„ ШӘЩҶШёЫҢЩ…ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШЁШ§ Ш§Ш¶Ш§ЩҒШ§ШӘ:
В
В
|
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|
В |
В |
В |
В |
В |
В |
В |
1209 |
|
1214 |
1218 |
1222 |
1226 |
1230 |
1234 |
1238 |
***** |
|
1243 |
1247 |
1251 |
1255 |
1259 |
1263 |
1267 |
1271 |
|
1276 |
1280 |
1284 |
1288 |
1292 |
1296 |
1300 |
1304 |
|
1309 |
1313 |
1317 |
1321 |
1325 |
1329 |
1333 |
1337 |
|
1342 |
1346 |
1350 |
1354 |
1358 |
1362 |
1366 |
***** |
|
1371 |
1375 |
1379 |
1383 |
В |
В |
В |
В |
В
В
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШҜЩҲ Щ…ЩҲШұШҜ Ш§Ш®ШӘЩ„Ш§ЩҒ ШЁЫҢЩҶ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ ЩҲ Ш¬ШҜЩҲЩ„ ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ Ъ©ЩҮ ЫҢЪ©ЫҢ Ш§ЩҒШІЩҲШҜЩҶ ШіШ§Щ„вҖҢЩҮШ§ЫҢ ШЁШ№ШҜ Ш§ШІ 1366Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ ЩҶЫҢШіШӘ ЩҲЩ„ЫҢ ШЁЩҮ ШөЩҲШұШӘ Щ…ШӘЩҶ ШӘЩҲШ¶ЫҢШӯ ШҜШұ ШөЩҒШӯЩҮ 121 Ъ©ШӘШ§ШЁ Ш§ЫҢШҙШ§ЩҶ ШўЩ…ШҜЩҮ Ш§ШіШӘШҢ ЩҲ ШҜЩҲ ШіШ§Щ„ Ш§ЩҲЩ„ Ш¬ШҜЩҲЩ„ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ 1214 ЩҲ 1218 Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ш§ЫҢШҙШ§ЩҶ Ш¬Ш§ЫҢШҙ Ш®Ш§Щ„ЫҢ ШЁЩҲШҜ ЩҲЩ„ЫҢ Щ…ЩҶ ШӘЪ©Щ…ЫҢЩ„ Ъ©ШұШҜЩ… ШӘШ§ ШЁЩҮ ШіШ§Щ„ ЩҫШ§ЫҢШ§ЩҶЫҢ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ЩӮШЁЩ„ЫҢ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 1209 ШЁШұШіШҜ.
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁШ§ ШЁШ§ШІЪҜШҙШӘ ШЁЩҮ Ш№ЩӮШЁ ЫҢШ§ Ш§ШІ Ш·ШұЫҢЩӮ Щ…ШӯШ§ШіШЁШ§ШӘ ЩӮЩҮЩӮШұШ§ЫҢЫҢ ШЁЩҮ ШўШәШ§ШІ ЫҢШ§ Щ…ШЁШҜШ§ЫҢЫҢ ШЁШұШіЫҢЩ… Ъ©ЩҮ ЩҫШі Ш§ШІ ЪҜШ°ШҙШӘ ЪҶЩҶШҜЫҢЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁЩҮ ШіШ§Щ„ 1209 ЩҲ ШЁШ№ШҜ ШЁЩҮ ШіШ§Щ„ 1337 ШұШіЫҢШҜЩҮ Ш§ШіШӘ:
Ш§ЫҢЩҶ Ш№Щ…Щ„ ШұШ§ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁЩҮ ШҜЩҲ Ш·ШұЫҢЩӮ Ш§ЩҶШ¬Ш§Щ… ШҜШ§ШҜ: ЩҶШ®ШіШӘ ШЁШ§ Ъ©ШіШұ 128 ШіШ§Щ„ 128 ШіШ§Щ„ Ш§ШІ ЩҮШұ ЫҢЪ© Ш§ШІ ШіШ§Щ„ ЩҮШ§ЫҢ 1337 ЫҢШ§ 1209ШҢ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
1337-1209-1081-953-825-697-569-441-313-185-57
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁЩҮ ШіШ§Щ„ 57 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…ЫҢвҖҢШұШіЫҢЩ… Ъ©ЩҮ Ш§ЪҜШұ Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШұШ§ ШЁЩҮ ЪҜЩҲЩҶЩҮ ШҜЫҢЪҜШұ Ш§Щ…ШӘШӯШ§ЩҶ Ъ©ЩҶЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
57 +(128 Г—10 )=128 Г·1337
ЩҲЩ„ЫҢ Ш§ШІ ШўЩҶ Ш¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ШіШ§Ші Ш§ЫҢЩҶ Щ…ШӯШ§ШіШЁЩҮ ШЁШұ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШЁШ§ЫҢШҜ ШұЩӮЩ… ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ ЫҢШ№ЩҶЫҢ 57 ШұШ§ ШЁЩҮ ЪҜЩҲЩҶЩҮ Ш§ЫҢ ШЁЩҮ 128 ШіШ§Щ„ ШұШіШ§ЩҶШҜ ШҢЪ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
71 = 57 - 128
ЫҢШ§ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
128 = 57 + 71
В ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ш§ШіШ§Ші Ш§ЫҢЩҶ ЩҶЩҲШ№ Щ…ШӯШ§ШіШЁЩҮ ЩҲ Ш¬ШҜЩҲЩ„ ШЁЩҶШҜЫҢвҖҢЩҮШ§ Ъ©ЩҮ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ШЁЩҮ 71 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ШЁШұ Щ…ЫҢвҖҢЪҜШұШҜШҜ. ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Ш§ШіШӘ.
ШӯШ§Щ„ ШҜШұ Щ…ЩҲШұШҜ Ш§ЫҢЩҶ Ъ©ЩҮ ЪҶШұШ§ ШЁШ§ЫҢШҜ ШҜШұ Щ…ШӯШ§ШіШЁШ§ШӘ Ш®ЩҲШҜ 71 ШіШ§Щ„ ШЁШұ ШіШ§Щ„вҖҢЩҮШ§ЫҢ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш§ЩҒШІЩҲШҜ Щ…ЩҶ ШҜШұ Ш¬Ш§ЫҢЫҢ ЪҶЫҢШІЫҢ ЩҶШҜЫҢШҜЩҮвҖҢШ§Щ…В ЩҲ ЩҒЪ©Шұ Щ…ЫҢ Ъ©ЩҶЩ… Ш§ШіШ§Ші ЪҶЩҶЫҢЩҶ ШұЩӮЩ…ЫҢ ШЁШ§ЫҢШҜ ЪҜЩҒШӘШ§Шұ Ш§ШЁЩҲШұЫҢШӯШ§ЩҶ ШЁЫҢШұЩҲЩҶЫҢ ШЁШ§ШҙШҜ Ъ©ЩҮ ЪҜЩҒШӘЩҮ Ш§ШіШӘ Ш§ЫҢШұШ§ЩҶЫҢШ§ЩҶ 70 ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш®ЩҲШҜ ШұШ§ ЩҒШұШ§Щ…ЩҲШҙ Ъ©ШұШҜЩҮ ШЁЩҲШҜЩҶШҜ.
ЩҲЩ„ЫҢ ШЁШ§ Ш§ЫҢЩҶ ЩҲШ¬ЩҲШҜ ШЁШ§ Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ ЩҮЩ…ЫҢЩҶ 71 ШіШ§Щ„ Ш§ЩҒШІЩҲШҜЩҮ ЩҮЩ… ШЁЩҮ ШұШ§ШӯШӘЫҢ ШҜШұЫҢШ§ЩҒШӘ Ъ©ЩҮ Ш¬ШҜЩҲЩ„ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШӘЩҶШ·ЫҢЩ…ЫҢ Ш§ЫҢЩҶ Ш№ШІЫҢШІШ§ЩҶ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ ЪҶШұШ§ Ъ©ЩҮ Ш§ШөЩ„ ШұШ§ ШЁШұ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ ЪҜШ°Ш§ШҙШӘЩҮвҖҢШ§ЩҶШҜ ЩҲ ЪҜШұЩҶЩҮ ШЁШ§ ШұШіЫҢШҜЩҶ ШЁЩҮ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶШіШӘЩҶШҜ ШЁЩҮ ШұШ§ШӯШӘЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ъ©ЩҶЩҶШҜ. ЪҶШұШ§ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ ШҜШұ Щ…ЩҲШұШҜ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ЫҢШ§ ЩҶШЁЩҲШҜЩҶ Ш§ЫҢЩҶ ШіШ§Щ„1242 Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁШ§ Ш§ЩҒШІЩҲШҜЩҶ 71 ШіШ§Щ„ ШЁШұ ШұЩӮЩ… ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ ( ЩҲ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ ШіШ§Щ„ 1242) ШЁЩҮ ШҙШұШӯ ШІЫҢШұ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҫШұШҜШ§Ш®ШӘ:
1313= 71 + 1242
479563 = 2422 /365Г— 1313
479197 =В 2422 /365 Г—1312
366 =В 479197 вҖ“ 479563
Ъ©ЩҮ ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁШ§ШІ Ш§ШІ Щ…ШЁШҜШ§ 71 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ЩҶЫҢШІ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢЪ©ЩҶЫҢЩ… Ъ©ЩҮ ШіШ§Щ„ 1242 ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
ЩҮЩ…ЫҢЩҶ Ш·ЩҲШұ ШЁШ§ ШўШІЩ…Ш§ЫҢШҙ Ш§ШІ Ш·ШұЫҢЩӮ Ш§ШіШӘЩҒШ§ШҜЩҮ Ш§ШІ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
640 +(673 Г—1 )=673 Г· 1313
( - 0 - ) +( 128Г—5 )= 128 Г· 640
ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ ЪҶЩҲЩҶ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Щ…ШӯШ§ШіШЁЩҮ ШөЩҒШұ (ЫҢШ§ ЩҮЩ…Ш§ЩҶ 128) Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜШҢ ЩҫШі ШіШ§Щ„ 1242 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (1313) ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ЩҶЩҮ ШіШ§Щ„ 1243ШҢ ЩҮЩ…ЪҶЩҶЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШўЩҶ Ш®Ш§ЩҶЩҮ 128 Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ШіШӘ. ЩҲЩ„ЫҢ ЩӮШЁЩ„Ш§ ШҜЫҢШҜЫҢЩ… Ъ©ЩҮ ШЁШ§ Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ (1128 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ) Ш¬Ш§ЫҢЪҜШ§ЩҮ ШҜШұШіШӘ ШўЩҶ ШҜШұ Ш®Ш§ЩҶЩҮ 95 Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ЩӮШұШ§Шұ ШҜШ§ШұШҜ. ЩҲ ЩҮЩ…ЫҢЩҶ ЩҶЩ…ЩҲЩҶЩҮ ЩҲ ШўШІЩ…Ш§ЫҢШҙвҖҢЩҮШ§ЫҢ Щ…ШҙШ§ШЁЩҮ ЩҶШҙШ§ЩҶ Щ…ЫҢ ШҜЩҮШҜ Ъ©ЩҮ ШіШ§Щ„ 71 ЩҫЫҢШҙ Ш§ШІ Щ…ЫҢЩ„Ш§ШҜ ШҜШұ Щ…ШұШҜ ШӘШ№ЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҶШ§ШұШіШ§ШіШӘ ЩҲ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ Ш§ШӘЪ©Ш§ЫҢ ШўЩҶ ШЁЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҫШұШҜШ§Ш®ШӘ.
В ЩҮЩ…ЫҢЩҶ Ш·ЩҲШұ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШҜШұШіШӘЫҢ ЫҢШ§ ЩҶШ§ШҜШұШіШӘ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„ 1242 ЩҮШ¬ШұЫҢВ ШҙЩ…ШіЫҢ ШұШ§ ШЁШ§ Щ…ШЁШҜШ§ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ЩҶЫҢШІ Щ…ШӯШ§ШіШЁЩҮ Ъ©ШұШҜШҢ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
3588 = 2346 + 1242
1310489= 2422 /365Г—3588
1310123 =В 2422 /365 Г—3587
366 = 1310123 вҖ“ 1310489
223 + (673Г—5 )= 673 Г· 3588
95В + (128Г—1 )=128 Г· 223
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШӯШӘЫҢ ШЁШ§ Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ Щ…ШЁШҜШ§ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ЩҶЫҢШІ ШіШ§Щ„ 1242 ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ. ЫҢШ№ЩҶЫҢ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұЫҢ Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШЁШ§Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ (1128) ЩҲ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ШҜШұ ШЁШ§Щ„Ш§ ШҜЫҢШҜЫҢЩ… ШіШ§Щ„ 1342 Щ…Ш·Ш§ШЁЩӮ ШЁШ§ ШіШ§Щ„ 2470 Ш§ЫҢШұШ§ЩҶЫҢ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШўЩҶ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ ШҜШұ Ш®Ш§ЩҶЩҮ 95 ЩӮШұШ§Шұ ШҜШ§ШұШҜ.
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ Ш¬ШҜЩҲЩ„ ШӘЩҶШ·ЫҢЩ…ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШҜШұ Ъ©ШӘШ§ШЁ ШІЫҢШ¬ Щ…Щ„Ъ© ШЁШұШ§ЫҢ ШҜЩҲШұЩҮ 1222 ШӘШ§ 1366 ЩҲ ШӘЩҲШ¶ЫҢШӯШ§ШӘ ШӘЪ©Щ…ЫҢЩ„ЫҢ ШЁШ№ШҜ Ш§ШІ ШўЩҶ Ш§ЫҢШҙШ§ЩҶ ШҜШұ Щ…ЩҲШұШҜ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„ 1371 ШҜШұШіШӘ ЩҶЫҢШіШӘ ЩҲ ШЁШ§ ШӘШ№ЫҢЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШҜЩӮЫҢЩӮ ШіШ§Щ„вҖҢЩҮШ§ЫҢ 1242ШҢ 1275 ШҢ1304 ШҢ1309 ЩҲ 1370 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮШҢ ШЁШ§ЫҢШҜ ШЁЩҮ Ш§ШөЩ„Ш§Шӯ ШўЩҶ Ш§ЩӮШҜШ§Щ… Ъ©ШұШҜ Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ Ш¬ШҜЩҲЩ„ЫҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ Ъ©ЩҮ ШҜШұ ШўЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШҜШұШіШӘ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЩҒЩҲЩӮ Ш§Щ„Ш°Ъ©Шұ ЩҲ ШЁЩӮЫҢЩҮ ШіШ§Щ„ ЩҮШ§ЫҢ ШҜЩҲШұЩҮ Щ…ЩҲШұШҜ ШЁШӯШ« ШЁЩҮ ШұЩҲШҙЩҶЫҢ Щ…ШҙШ®Шө ЩҲ Щ…Ш№ЫҢЩҶ ШҙШҜЩҮ Ш§ШіШӘ.
В Ш·ШұШӯ Ш§ШөЩ„Ш§Шӯ ШҙШҜЩҮЩ” Ш¬ШҜЩҲЩ„ ШӘЩҶШ·ЫҢЩ…ЫҢ ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ©
В
В
|
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|
В |
В |
В |
В |
В |
В |
В |
******* |
|
В |
В |
В |
В |
В |
В |
В |
1209 |
|
1214 |
1218 |
1222 |
1226 |
1230 |
1234 |
1238 |
1242 |
|
1247 |
1251 |
1255 |
1259 |
1263 |
1267 |
1271 |
1275 |
|
1280 |
1284 |
1288 |
1292 |
1296 |
1300 |
1304 |
********* |
|
1309 |
1313 |
1317 |
1321 |
1325 |
1329 |
1333 |
1337 |
|
1342 |
1346 |
1350 |
1354 |
1358 |
1362 |
1366 |
1370 |
|
1375 |
1379 |
1383 |
1387 |
В |
В |
В |
В |
В
В
ШөШӯШӘ Щ…ШӯШ§ШіШЁШ§ШӘ ШұЫҢШ§Ш¶ЫҢ ЩҮЫҢЪҶ ШұШЁШ·ЫҢ ШЁЩҮ ШҜШұШіШӘЫҢ Щ…ШЁШҜШ§ Ш§ШЁШҜШ§Ш№ЫҢ ЩҲ Щ…ЩҶ ШҜШұШўЩҲШұШҜЫҢ Ш§ЩӮШ§ЫҢ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ЩҶШҜШ§ШұШҜ ЩҲ ЩҶШ§ШҜШұШіШӘЫҢ ШўЩҶ ЩҲЩҶЫҢШІ ШҜЩҲШұЩҮ 2820 ШіШ§Щ„ЩҮ Ш§ЫҢШҙШ§ЩҶ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШЁЩҮ ШӘЩҒШөЫҢЩ„ ШҜШұ Ъ©ШӘШ§ШЁ ШІШұШҜШҙШӘ ЩҲ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ Щ…ЩҲШұШҜ ШЁШӯШ« ЩӮШұШ§Шұ ЪҜШұЩҒШӘЩҮ Ш§ШіШӘ . ЩҲЩ„ЫҢ Ш§ШІ ШўЩҶ Ш¬Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ЫҢЩҶ Щ…ШЁШҜШ§ 2346 ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ЫҢЪ© Щ…ШЁШҜШ§ ШұЫҢШ§Ш¶ЫҢ ЩҲ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ Ш§ШіШӘ ШЁШҜЫҢЩҮЫҢ Ш§ШіШӘ Ъ©ЩҮ ШЁЩҮ Щ…ШӯШ§ШіШЁШ§ШӘ ШұЫҢШ§Ш¶ЫҢ ЩҫШ§ШіШ® Щ…ЫҢ ШҜЩҮШҜ .
ЩҮЩ…ЫҢЩҶ ЪҜЩҲЩҶЩҮ Ш§ШіШӘ ШЁШ§ШІ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ 71 ШіШ§Щ„ЩҮ Ъ©ЩҮ ШЁШ§ШІ ШҜШұ ШөЩҲШұШӘ Ш§ШІЩ…Ш§ЫҢШҙ ШҜШұ Ш®ЩҲШ§ЩҮЫҢЩ… ЫҢШ§ЩҒШӘ Ъ©ЩҮ ЩҮЩ…ЫҢШҙЩҮ ЩҲШҜШұ ЩҮЩ…ЩҮ Ш¬Ш§ ЩҫШ§ШіШ® ЪҜЩҲ ЩҶЫҢШіШӘ ЩҲ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ Ш§ШӘЪ©Ш§ЫҢ ШўЩҶ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ъ©Ш§Щ…Щ„ ЩҫШұШҜШ§Ш®ШӘ.
ШӯШ§Щ„ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШұЩҲШҙЩҶ ШҙШҜЩҶ Ъ©ШЁЫҢШіЩҮ ЫҢШ§ Ъ©ШЁЫҢШіЩҮ ЩҶШЁЩҲШҜЩҶ ШіШ§Щ„ ЩҮШ§ЫҢ ШҢ1242ШҢ 1276ШҢ 1371 ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ЩҲШ§ЩӮШ№ЫҢ Ш§ЫҢЩҶ ШіШ§Щ„ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮШҢ Ш¬ШҜЩҲЩ„ ШӘЩҶШ·ЫҢЩ…ЫҢ ШұШӯЫҢЩ… ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ© ШЁШұШ§ЫҢ ШҜЩҲШұЩҮ 1222 ШӘШ§ 1366 ЩҲ Ш§ШҜШ§Щ…ЩҮ ШўЩҶ ШӘШ§ ШіШ§Щ„ 1383ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШұШ§ ШЁШ§ЫҢШҜ ШЁЩҮ ШөЩҲШұШӘ ШІЫҢШұ Ш§ШөЩ„Ш§Шӯ Ъ©ШұШҜ.
В Ш·ШұШӯ Ш§ШөЩ„Ш§Шӯ ШҙШҜЩҮЩ” Ш¬ШҜЩҲЩ„ ШӘЩҶШ·ЫҢЩ…ЫҢ ШұШ¶Ш§ ШІШ§ШҜЩҮ Щ…Щ„Ъ©
В
В
|
5ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
4ШіШ§Щ„ЩҮ |
|
В |
В |
В |
В |
В |
В |
В |
******* |
|
В |
В |
В |
В |
В |
В |
В |
1209 |
|
1214 |
1218 |
1222 |
1226 |
1230 |
1234 |
1238 |
1242 |
|
1247 |
1251 |
1255 |
1259 |
1263 |
1267 |
1271 |
1275 |
|
1280 |
1284 |
1288 |
1292 |
1296 |
1300 |
1304 |
********* |
|
1309 |
1313 |
1317 |
1321 |
1325 |
1329 |
1333 |
1337 |
|
1342 |
1346 |
1350 |
1354 |
1358 |
1362 |
1366 |
1370 |
|
1375 |
1379 |
1383 |
1387 |
В |
В |
В |
В |
В
В
ШЁШҜЫҢЩҶ ЪҜЩҲЩҶЩҮ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢ ЩҒШұЩ…Ш§ЫҢЩҶШҜ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ 71 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ЩҲ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ш«Ш§ШЁШӘ 128 ШіШ§Щ„ЩҮ Ш§Щ…ШұЫҢ ЩҶШ§ШұШіШ§ ЩҲ ЩҶШ§ШҜШұШіШӘ Ш§ШіШӘ. ЩҮЩ…ЫҢЩҶ ЩҲШ¶Ш№ЫҢШӘ ШұШ§ ШЁШ§ШІ ШҜШұ ШөЩҲШұШӘ Щ…ЩӮШ§ЫҢШіЩҮ ЩҲШӘШ·ШЁЫҢЩӮ Щ…ШЁШҜШ§ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ Ш§Щ„ШЁШӘЩҮ ШЁШ§ Ш§Ш®ШӘЩ„Ш§ЩҒ ЩҮШ§ЫҢЫҢ ШЁЩҮ Щ…ШұШ§ШӘШЁ Ъ©Щ… ШӘШұ Щ…ШҙШ§ЩҮШҜЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ШұШҜ.
Ш№Щ„ШӘ Ш§ЫҢЩҶ Ш§Щ…Шұ ШҜШұ ШӯЩӮЫҢЩӮШӘ Щ…ШӘЩҒШ§ЩҲШӘ ШЁЩҲШҜЩҶ ШўШәШ§ШІ Ш§ЫҢЩҶ Щ…ШЁШҜШ§ ЩҮШ§ЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ ШЁШ§ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ ЫҢШ§ ЩҮЩ…Ш§ЩҶ Щ…ШЁШҜШ§ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ШІШұШҜШҙШӘ ШҜШұ ШіШ§Щ„ 1128 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ Ш§ШіШӘ.
ЩҲ ШЁШ§ШІ ШЁЩҮ Ш®Ш§Ш·Шұ ЩҮЩ…ЫҢЩҶ Ш№ШҜЩ… Щ…Ш·Ш§ШЁЩӮШӘ Ш§ЫҢЩҶ Щ…ШЁШҜШЈЩҮШ§ШіШӘ Ъ©ЩҮ Ш№Щ…Щ„Ш§ ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШўЩҶвҖҢЩҮШ§ ШұШ§ ШЁШ§ ЩҮЩ… ШӘШ·ШЁЫҢЩӮ ШҜШ§ШҜ. ШЁШұШ§ЫҢ ЩҶЩ…ЩҲЩҶЩҮ ЩҲ ШЁШұШ§ЫҢ ШұЩҲШҙЩҶ ШҙШҜЩҶ Ш§ЫҢЩҶ Ш§Ш®ШӘЩ„Ш§ЩҒвҖҢЩҮШ§ ШҜШұ Ш§ЫҢЩҶШ¬Ш§ ЩҒЩҮШұШіШӘ ШӘШ·ШЁЫҢЩӮЫҢ Ш§ЫҢЩҶ Щ…ШЁШҜШ§ ЩҮШ§ЫҢ Щ…ШӘЩҒШ§ЩҲШӘ ШЁШ§ЩҮЩ… ШұШ§ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128ШіШ§Щ„ЩҮШҢ Ш§ШІ ШіШ§Щ„ 57 ЩҮШ¬ШұШӘ ШЁЩҮ ШөЩҲШұШӘ ЫҢЪ© Ш¬ШҜЩҲЩ„ Щ…ЫҢ ШўЩҲШұЫҢЩ…:
ЩҒЩҮШұШіШӘ ШӘШ·ШЁЫҢЩӮЫҢ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ
В
В
|
ШұШҜЫҢЩҒ |
ШӘШ§ШұЫҢШ® ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ |
ШЁШұШ§ШіШ§Ші Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ(Ш®.Ш§.) (1128) |
ШЁШұШ§ШіШ§Ші Щ…ШЁШҜШ§ Ш°ШЁЫҢШӯ ШЁЩҮШұЩҲШІ ( 2346) |
ШЁШұ Ш§ШіШ§Ші 71 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ |
|
1 |
57 |
1185 |
2403 |
128 |
|
2 |
185 |
1313 |
2531 |
256 |
|
3 |
218 |
1346 |
2564 |
289 |
|
4 |
346 |
1474 |
2692 |
417 |
|
5 |
474 |
1602 |
2820 |
545 |
|
6 |
602 |
1730 |
2948 |
673 |
|
7 |
730 |
1858 |
3076 |
801 |
|
8 |
858 |
1986 |
3204 |
929 |
|
9 |
891 |
2019 |
3237 |
962 |
|
10 |
1019 |
2147 |
3365 |
1090 |
|
11 |
1147 |
2275 |
3493 |
1218 |
|
12 |
1275 |
2403 |
3621 |
1346 |
|
13 |
1403 |
2531 |
3749 |
1474 |
В
В
В Ш§ЪҜШұ ШҜШұ Ш§ЫҢЩҶ ЪҶЩҮШ§Шұ ШіШӘЩҲЩҶ ШҜЩӮШӘ Ъ©ЩҶЫҢЩ…ШҢ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜЫҢШҜ ЪҜШұЪҶЩҮ Ш§ЫҢЩҶ ЪҶЩҮШ§Шұ ШіШӘЩҲЩҶ ШҜШ§ШұШ§ЫҢ Щ…ШЁШҜШ§ Щ…ШӘЩҒШ§ЩҲШӘЫҢ ЩҮШіШӘЩҶШҜ ШЁШ§ Ш§ЫҢЩҶ ЩҲШ¬ЩҲШҜ ШҜШұ ЩҮШұ ШіШӘЩҲЩҶ ШЁШ§ ШҜЩҲ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ 673 ШіШ§Щ„ЩҮ ШұЩҲШЁШұЩҲ ЩҮШіШӘЫҢЩ…ШҢВ Ъ©ЩҮ Ш№ШЁШ§ШұШӘЩҶШҜ Ш§ШІ:
ШіШ§Щ„ ЩҮШ§ЫҢ 218 ЩҲ891 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШҜШұ ШіШӘЩҲЩҶ ШҜЩҲЩ….В В В В В В В В В В В В В В В В В В В
ШіШ§Щ„ ЩҮШ§ЫҢ 1346 ЩҲ2019 Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§ЫҢШұШ§ЩҶЫҢ ШҜШұ ШіШӘЩҲЩҶ ШіЩҲЩ….В В В В В В В В В В В В
ШіШ§Щ„ ЩҮШ§ЫҢ 2692ЩҲ3365Ш®ЩҲШұШҙЫҢШҜЫҢ ШҙЩҮШұЫҢШ§ШұЫҢ ШҜШұ ШіШӘЩҲЩҶ ЪҶЩҮШ§ШұЩ….В В В В В В В В
ШіШ§Щ„ ЩҮШ§ЫҢ 673ЩҲ1346ШҜШұ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШЁШ№Щ„Ш§ЩҲЩҮ 71 ШіШ§Щ„ ШҜШұШіШӘЩҲЩҶ ШўШ®Шұ
В ШЁШ§ ЩҲШ¬ЩҲШҜ Ш§ЫҢЩҶ ШҜШұ ШіШӘЩҲЩҶ ЪҶЩҮШ§ШұЩ… ШҜЩҲ ШіШ§Щ„ 2564 ЩҲ 3237ШҜШұ ШөЩҲШұШӘ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ 673 ШіШ§Щ„ЩҮ ШЁЩҮ ШҜЩ„ЫҢЩ„ Ш§ЫҢЩҶ Ъ©ЩҮ ШұЩӮЩ… ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ ШўЩҶ ЩҮШ§ 33 ШіШ§Щ„ Ш§ШіШӘ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ЩҲЩ„ЫҢ Ш§ЪҜШұ ЩҮЩ…ЫҢЩҶ ШҜЩҲ ШіШ§Щ„ Ш§ШІ Ш·ШұЫҢЩӮ Щ…ШӯШ§ШіШЁЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ЩҲШұШҜ ШўШІЩ…Ш§ЫҢШҙ ЩӮШұШ§Шұ ШҜЩҮЫҢЩ… Ш®ЩҲШ§ЩҮЫҢЩ… ШҜЫҢШҜ Ъ©ЩҮ ШҜШ§ШұШ§ЫҢ 366 ШұЩҲШІ ЩҮШіШӘЩҶШҜ ЩҲ ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ШЁШ§ЫҢШҜ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙЩҶШҜ. ЩҲЩ„ЫҢ ШҜШұ ШіШӘЩҲЩҶ ЩҫЩҶШ¬Щ… ШҢ ШҜШұ ШөЩҲШұШӘ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… Ъ©ШұШҜ Ъ©ЩҮ ШӘШ№ШҜШ§ШҜ ЩҫЩҶШ¬ ШіШ§Щ„ Ш§ШІШіШ§Щ„ ЩҮШ§ЫҢ Ш§ЫҢЩҶ ШіШӘЩҲЩҶ ШЁШ§ШІ ШЁЩҮ ШҜЩ„ЫҢЩ„ Ш§ЫҢЩҶ Ъ©ЩҮ ШҜШ§ШұШ§ЫҢ ШЁШ§ЩӮЫҢЩ…Ш§ЩҶШҜЩҮ 33 ШіШ§Щ„ЩҮ Щ…ЫҢ ШҙЩҲЩҶШҜ ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙЩҶШҜ. ШҜШұ ШөЩҲШұШӘЫҢ Ъ©ЩҮ ЩҮЩ…ЫҢЩҶ ЩҫЩҶШ¬ ШіШ§Щ„ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Ш§ЫҢ ЩҮШіШӘЩҶШҜ ЩҲ Ш§ЫҢЩҶ ЩҫЩҶШ¬ ШіШ§Щ„ Ш№ШЁШ§ШұШӘЩҶШҜ Ш§ШІ: ШіШ§Щ„вҖҢЩҮШ§ЫҢ 289ШҢ 417 ШҢ962 ШҢ1090 ЩҲ 1218 ШЁШ§ Ш§ЫҢЩҶ ЩҲШ¬ЩҲШҜ ШЁШ§ ШӘЩ…Ш§Щ… ШӘЩҒШ§ЩҲШӘ Щ…ШЁШҜШЈЩҮШ§ЫҢЫҢ Ъ©ЩҮ ШҜШұ ШіЩҮ ШұЩҲШҙ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ ШЁШ§Щ„Ш§ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜШҢ ШЁШ§ Ъ©Щ…Ш§Щ„ ШӘШ№Ш¬ШЁ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜЫҢШҜ Ъ©ЩҮ ШЁШұШ§ШіШ§Ші ЩҮЩ…ЫҢЩҶ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШ§ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128ШіШ§Щ„ЩҮ ШҜШұ ШҜЩҲШұЩҮ Ш§Ш®ЫҢШұ Ъ©ШЁЫҢШіЩҮВ 128 ШіШ§Щ„ЩҮ ЫҢШ№ЩҶЫҢ Ш§ШІ ШіШ§Щ„ 1275 ШӘШ§ 1403 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢШҢ ЩҶШӘЫҢШ¬ЩҮ ЩҮЩ…ЩҮ ЫҢЪ©ШіШ§ЩҶ Ш®ЩҲШ§ЩҮШҜШЁЩҲШҜ ЪҶЩҮ Ш§ШІ ЩҶШёШұ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШҢ ЪҶЩҮ Ш§ШІ ЩҶШёШұ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ.
ШЁЩҮ Ш®Ш§Ш·Шұ ЩҮЩ…ЫҢЩҶ Ш§ШӘЩҒШ§ЩӮ ШҙЪҜЩҒШӘ ЩҲЩҶЫҢШІШўШҙЩҶШ§ЫҢЫҢ ШЁШ§ ЩҶЩҲШ№ Щ…ШӯШ§ШіШЁЩҮ Ш§ЫҢЩҶ ШіШ§Щ„ ЩҮШ§ Ш§ШІ ШіШ§Щ„ 1275 ШӘШ§ ШіШ§Щ„1403 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…Ш·Ш§ШЁЩӮ ШЁШ§ 2403 ШӘШ§ 2531 Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§ЫҢШұШ§ЩҶЫҢВ ЩҲ ШҜЩҲ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ 2346 ЩҲ71 ШіШ§Щ„ЩҮ Щ…ШӯШ§ШіШЁЩҮ ЩҲ ШӘШ·ШЁЫҢЩӮ ШҜШ§ШҜЩҮ ЩҲ ШӯШ§ШөЩ„ Щ…ШӯШ§ШіШЁШ§ШӘ Ш®ЩҲШҜ ШұШ§ ШЁЩҮ ШөЩҲШұШӘ ШҜЩҲ Ш¬ШҜЩҲЩ„ Ш¬ШҜШ§ЪҜШ§ЩҶЩҮ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ Щ…ЫҢ ШўЩҲШұЫҢЩ… ШҢЪ©ЩҮ ШЁШұ Ш§ШіШ§Ші ШўЩҶ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ ШұШ§ШӯШӘЫҢ ШҜШұЫҢШ§ЩҒШӘ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Ъ©ШЁЫҢШіЩҮвҖҢЪҜЫҢШұЫҢ ШЁШұ Ш§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ЩҲ 128 ШіШ§Щ„ЩҮШҢ ШҜШұ ЩҶЩҮШ§ЫҢШӘ ЩҶШӘЫҢШ¬ЩҮ ШӯШ§ШөЩ„ЩҮ ШҜШұ Щ…ЩҲШұШҜ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҶ ШіШ§Щ„ ЩҮШ§ЫҢ Щ…ШҙШ®Шө ШҜШұ ЩҮШұ ШіЩҮ Щ…ШЁШҜШ§ ЫҢЪ©ШіШ§ЩҶ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ. Ш§ЩҒШІЩҲЩҶ ШЁШұ Ш§ЫҢЩҶ Ъ©ЩҮ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЩҶЫҢШІ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЫҢЪ©ШіШ§ЩҶ Ш®ЩҲШ§ЩҮШҜ ШҙШҜ.
ШЁЩҮ ЪҜЩҲЩҶЩҮвҖҢШ§ЫҢ Ъ©ЩҮ ШҜШұ ЩҶЩҮШ§ЫҢШӘ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ ШЁШ№ШҜ Ш§ШІ ШўЩҶ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 1309 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ъ©ЩҮ Ш§ЩҲЩ„ЫҢ ЫҢЪ© Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ Ш§ШіШӘ ЩҲ ШҜЩҲЩ…ЫҢ ЫҢЪ© Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЩҮ ШӘШұШӘЫҢШЁ ШҜШұ Ш®Ш§ЩҶЩҮвҖҢЩҮШ§ЫҢ 29 ЩҲ 34 Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ ЩҲ ШЁШұ Ш§ЫҢЩҶ Ш§ШіШ§Ші Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1242 Ъ©ЩҮ ШЁШ§ШІ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш§ШіШӘ ШҜШұ Ш®Ш§ЩҶЩҮ 95 Ш¬ШҜЩҲЩ„ ЩӮШұШ§ШұШ®ЩҲШ§ЩҮШҜ ЪҜШұЩҒШӘ ЩҲ ЩҮЩ…ЪҶЩҶЫҢЩҶ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ 1370 Ъ©ЩҮ ШЁШ§ШІ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ Ш§ШіШӘ ШҜШұ Ш®Ш§ЩҶЩҮ 95 Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ . Ш§ЩҒШІЩҲЩҶ ШЁШұ Ш§ЫҢЩҶ Ъ©ЩҮ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ ШӘЩҶШёЫҢЩ…ЫҢ (ШІЫҢШұ) Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢ ШҙЩҲШҜ Ш§ЩҲЩ„ЫҢЩҶ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Ш§Ш®ЫҢШұ ШіШ§Щ„ 1280 Щ…ЫҢвҖҢШЁШ§ШҙШҜ. Ъ©ЩҮ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ Ш№ЫҢЩҶ Ш¬ШҜЩҲЩ„ ЩҮШ§ЫҢ ШӘШ·ШЁЫҢЩӮЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ Ш§ЫҢЩҶ ШҜЩҲШұЩҮ Шұ Ш§ ШЁШ§ ЩҮЩ… Щ…ЫҢ ШўЩҲШұЫҢЩ… ШӘШ§ ШӘШ·ШЁЫҢЩӮ ШўЩҶ ЩҮШ§ ШЁЩҮ ШұШ§ШӯШӘЫҢ ЩӮШ§ШЁЩ„ Щ…ШҙШ§ЩҮШҜЩҮ ШЁШ§ШҙШҜ:
В
Ш¬ШҜЩҲЩ„ Щ…ЩӮШ§ЫҢШіЩҮ Ш§ЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ Ш§ШІ ШіШ§Щ„ 1304 ШіШ§Щ„ ШўШәШ§ШІ Щ…ШЁШҜШў ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш¬ШҜЫҢШҜ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ ШІЫҢШұ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШЁШұ ЩҫШ§ЫҢЩҮ ЫҢ ШіЩҮ Щ…ШЁШҜШў Щ…ШӯШ§ШіШЁШ§ШӘЫҢ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ
В
В
|
В В ШұШҜЫҢЩҒВ |
ШҙЩ…Ш§ШұЩҮ ШіШ§Щ„ ШҜШұЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҮШ¬ШұЫҢВ В Ш®ЩҲШұШҙЫҢШҜЫҢ В |
В В 71+В В |
В В 1128+ |
В В 2346+ |
В ЩҶЩҲШ№ Ъ©ШЁЫҢШіЩҮ |
Ш¬Ш§ЫҢЪҜШ§ЩҮ ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШҜШұ Ш¬ШҜЩҲЩ„В Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128ШіШ§Щ„ЩҮ |
|
ЫҢЪ©В В В |
1304В В |
1375В |
2432В |
3650В |
4 ШіШ§Щ„ЩҮВ |
29В В В |
|
ШҜЩҲВ В В |
1309В В |
В 1380В |
2437В |
3655В |
5 ШіШ§Щ„ЩҮВ |
34В В В |
|
ШҜЩҲВ В В |
1313В В |
1384В |
2441В |
3659В |
4 ШіШ§Щ„ЩҮВ |
38В В В |
|
ШҜЩҲВ В В |
В В В 1317В В |
В 1388 |
В 2445 |
В 3663 |
4 ШіШ§Щ„ЩҮВ |
42В В В |
|
ШҜЩҲВ В В |
В В В В 1321В |
1392В |
2449В |
3667В |
4ШіШ§Щ„ЩҮВ |
46В В В |
|
ШҜЩҲВ В В |
В В В В 1325В |
1396В |
2453В |
3671В |
4 ШіШ§Щ„ЩҮВ |
50В В В |
|
ШҜЩҲВ В В |
1329В |
1400В |
2457В |
3675В |
4 ШіШ§Щ„ЩҮВ |
54В В В |
|
ШҜЩҲВ В В |
1333В |
1404В |
2461В |
3679В |
4 ШіШ§Щ„ЩҮВ |
58В В В |
|
ШҜЩҲВ В В |
1337В В |
1408В |
2465В |
3683В |
4ШіШ§Щ„ЩҮВ В |
62В В В |
|
ШіЩҮВ В В |
1342В В |
1413В |
2470В |
3688В |
5 ШіШ§Щ„ЩҮВ |
67В В В |
|
ШіЩҮВ В В |
1346В В |
1417В |
2474В |
3692В |
4 ШіШ§Щ„ЩҮВ |
71В В В |
|
ШіЩҮВ В В |
1350В В |
1421В |
2478В |
В 3696 |
4 ШіШ§Щ„ЩҮВ |
75В В В |
|
ШіЩҮВ В В |
1354В В |
1425В |
2482В |
В 3700 |
4 ШіШ§Щ„ЩҮВ |
79В В В |
|
ШіЩҮВ В В |
1358В В |
1429В |
2486В |
В 3704 |
4 ШіШ§Щ„ЩҮВ |
83В В В |
|
ШіЩҮВ В В |
1362В В |
1433В |
2490В |
В 3708 |
4 ШіШ§Щ„ЩҮВ |
87В В В |
|
ШіЩҮВ В В |
1366В В |
1437В |
2494В |
В 3712 |
4 ШіШ§Щ„ЩҮВ |
91В В В |
|
ШіЩҮВ В В |
1370В В |
1441В |
2498В |
В 3716 |
4 ШіШ§Щ„ЩҮВ |
95В В В |
|
ЪҶЩҮШ§ШұВ |
1375В В |
1446В |
В 2503В В |
В 3721 |
5 ШіШ§Щ„ЩҮВ |
100В В |
|
ЪҶЩҮШ§ШұВ |
1379В В |
1450В |
2507В |
В 3725 |
4 ШіШ§Щ„ЩҮВ |
104В В |
|
ЪҶЩҮШ§ШұВ |
1383В В |
1454В |
В В 2511 |
В 3729 |
4 ШіШ§Щ„ЩҮВ |
В В В 108В |
|
ЪҶЩҮШ§ШұВ |
1387В В |
1458В |
В 2515В |
В 3733 |
4 ШіШ§Щ„ЩҮВ |
112В В |
|
ЪҶЩҮШ§ШұВ В |
1391В В |
1462В |
В 2519 |
В 3737 |
4 ШіШ§Щ„ЩҮВ |
116В В |
|
ЪҶЩҮШ§ШұВ В |
1395В В |
1466В |
В 2523 |
В 3741 |
4 ШіШ§Щ„ЩҮВ |
120В В |
|
ЪҶЩҮШ§ШұВ В |
1399В В |
1470В |
В 2527 |
В 3745 |
4 ШіШ§Щ„ЩҮВ |
124В В |
|
ЪҶЩҮШ§ШұВ В |
1403В В |
1474В |
В 2531 |
В 3749 |
4 ШіШ§Щ„ЩҮВ |
128В В |
В
В
Ъ©ЩҮ Ш§ЫҢЩҶ Ш¬ШҜЩҲЩ„ Шұ Ш§ ЫҢЪ© Ш¬Ш§ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШЁЩҮ ШөЩҲШұШӘ Ш¬ШҜЩҲЩ„ ШІЫҢШұ ЩҶЩҲШҙШӘ Ш§Щ„ШЁШӘЩҮ Ш§ШІ ШіШ§Щ„ 1280 ЫҢШ№ЩҶЫҢ ШўШәШ§ШІ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Ш§Ш®ЫҢШұ.
В
В
|
ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
|
1280 1351 2408 3626 |
1284 1355 2412 3630 В |
В 1288В 1359В 2416В 3634В |
1292В 1363В 2420В 3638В |
1296В 1367В 2424В 3642В |
1300В 1371В 2428В 3646В |
1304 1375 2432 3650 |
****** ****** ****** ****** |
|
1309 1380В 2437В 3655В |
1313 1384 2441 3659 В |
1317 1388 2445 3663 |
1321В 1392В 2449В 3667В |
1325В 1396В 2453В 3671В |
1329В 1400В 2457В 3675В |
1333В 1404В 2461В 3679В |
1337 1408 2465 3683 |
|
1342В 1413В 2470В 3688В |
1346В 1417В 2474В 3692В |
1350В 1421 2478 3696 |
1354В 1425В 2482В 3700В |
1358В 1429В 2486В 3704В В |
1362В 1433В 2490В 3708В |
1366В 1437В 2494В 3712В |
1370В 1441В 2498В 3716В |
|
1375В 1446В 2503В 3721В |
1379В 1450В 2507В 3725В |
1383В 1454В 2511В 3729В |
1387В 1458В 2515В 3733В |
1391В 1462В 2519В 3737В |
1395В 1466В 2523В 3741В |
1399В 1470В 2527В 3745В |
1403В 1474В 2531В 3749В |
|
В В ****В |
****В |
****В |
****В |
****В |
****В |
****В |
****В |
В
В
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮВ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜШҢ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ ШҜЩҲ Ш¬ШҜЩҲЩ„ Ш¬ШҜШ§ЪҜШ§ЩҶЩҮ ШЁШұШ§ЫҢ ЫҢЪ© ШҜЩҲШұЩҮ ШӘЩҶШ·ЫҢЩ… ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ Ш§ЩҲЩ„ЫҢ ЫҢШ§ Ш¬ШҜЩҲЩ„ ШЁШ§Щ„Ш§ЫҢЫҢ Ъ©ЩҮ Ш§ШІ Ш§ЩҲЩ„ЫҢЩҶ ШіШ§Щ„ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ (1304) ШӘШ§ ЩҫШ§ЫҢШ§ЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Щ…Ш№Ш§ШөШұ ШұШ§ ШҜШұ ШЁШұ Щ…ЫҢ ЪҜЫҢШұШҜ ШҜШұ ЩҮШұ ШіШӘЩҲЩҶ Ш§ЩҒЩӮЫҢ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ ШҜШұ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШЁШ§ Щ…Ш№Ш§ШҜЩ„ ШўЩҶ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ ЩҲ ЩҶЫҢШІ Щ…ШЁШҜШ§ЩҮШ§ЫҢ Щ…ШӯШ§ШіШЁШ§ШӘЫҢ 71 ЩҲ 2346 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ШўЩ…ШҜЩҮ Ш§ШіШӘ ЩҲ ШҜШұ ШіШӘЩҲЩҶ ШўШ®Шұ ЩҶЫҢШІ Ш¬Ш§ЫҢЪҜШ§ЩҮ ЩҮШұ ШіШ§Щ„ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ШӘШ№ЫҢЩҶ ЩҲЩ…ШҙШ®Шө ШҙШҜЩҮ Ш§ШіШӘ (В ШЁШ§ Щ…ШӯШ§ШіШЁЩҮ Ш§ШІ Ш·ШұЫҢЩӮ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ЩҲ128 ШіШ§Щ„ЩҮ ) ЩҲ ШҜШұ Ш¬ШҜЩҲЩ„ ШҜЩҲЩ… Ъ©ЩҮ ШЁШұШ§ЫҢ Ъ©Щ„ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Щ…Ш№Ш§ШөШұ Ш§ШІ ШіШ§Щ„ 1280 ШӘШ§ 1403 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШӘЩҶШёЫҢЩ… ШҙШҜЩҮ Ш§ШіШӘ ШҜШұ ЩҮШұ Ш®Ш§ЩҶЩҮ ШЁЩҮ ШӘШұШӘЫҢШЁ ШӘШ§ШұЫҢШ® Щ…ЩҲШұШҜ ЩҶШ·Шұ ШҜШұ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ЩҲ ШЁЩӮЫҢЩҮ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЫҢШ§ Щ…ШЁШҜШ§ ЩҮШ§ ШЁЩҮ ШөЩҲШұШӘ ШІЫҢШұ ЩҮЩ… ШўЩ…ШҜЩҮ Ш§ШіШӘ ШӘШ§ ШӘШ·ШЁЫҢЩӮ ШўЩҶвҖҢЩҮШ§ ШҜЩӮЫҢЩӮШ§ Щ…ЩҲШұШҜ Щ…ШҙШ§ЩҮШҜЩҮ ШЁШ§ШҙШҜ.
Ш§ШІ ШіЩҲЫҢ ШҜЫҢЪҜШұ Щ…Ш№Щ„ЩҲЩ… ЩҶЫҢШіШӘ ЩҮЫҢШ§ШӘ ШӘЩҮЫҢЩҮ ЩҲ ШӘЩҶШёЫҢЩ… ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш¬ШҜЫҢШҜ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜШұ ШіШ§Щ„ 1304 ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШЁШұ ЪҶЩҮ Ш§ШіШ§Ші ЩҲ Щ…ШӯШ§ШіШЁЩҮ Ш§ЫҢ ШіШ§Щ„ 1304 ШұШ§ ЫҢЪ©ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЪҶЩҮШ§Шұ ШіШ§Щ„ЩҮ ЩҲ ЩҫЩҶШ¬ ШіШ§Щ„ ШЁШ№ШҜ ЫҢШ№ЩҶЫҢ ШіШ§Щ„ 1309 ШұШ§ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ ШЁЩҮ ШҙЩ…Ш§Шұ ШўЩҲШұШҜЩҮвҖҢШ§ЩҶШҜ. ШЁЩҲЫҢЪҳЩҮ ШўЩҶ Ъ©ЩҮ ШіЫҢШҜ ШӯШіЩҶ ШӘЩӮЫҢ ШІШ§ШҜЩҮ Ъ©ЩҮ Ш®ЩҲШҜ Ш·ШұШ§Шӯ ЩҲ ЩҫЫҢШҙЩҶЩҮШ§ШҜ ШҜЩҮЩҶШҜЩҮ Ш§ШөЩ„ЫҢ Ш§ЫҢЩҶ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ШіШӘ (ЩҶШҙШұЫҢЩҮ Ъ©Ш§ЩҲЩҮ) ШҜШұ ЩҮЫҢЪҶ Ш¬Ш§ЫҢ Ъ©ШӘШ§ШЁ ЩҮШ§ ЩҲЩ…ЩӮШ§Щ„ЩҮвҖҢЩҮШ§ЫҢ Ш®ЩҲШҜ ШҜШұ Щ…ЩҲШұШҜ Ш§ЫҢЩҶ Щ…ЩҲШ¶ЩҲШ№ Ш§ШҙШ§ШұЩҮвҖҢШ§ЫҢ ЩҶЪ©ШұШҜЩҮ Ш§ШіШӘ. Ш№Щ„Ш§ЩҲЩҮ ШЁШұШўЩҶ ШҜШұ ЩӮШ§ЩҶЩҲЩҶ ШӘШөЩҲЫҢШЁ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШҜШұ ШіШ§Щ„ 1304 ЩҶЫҢШІ ЩҮЫҢЪҶ Ш§ШҙШ§ШұЩҮвҖҢШ§ЫҢ ШЁЩҮ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ЩҲ ШұЩҲШҙ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШҜШұ Ш§ЫҢЩҶ ШӘЩӮЩҲЫҢЩ… ЩҶШҙШҜЩҮ Ш§ШіШӘ. ЩҲ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ ЩҫЫҢШҙ Ш§ШІШ§ЫҢЩҶ ЫҢШ§ШҜ ШўЩҲШұШҙШҜЫҢЩ…ШҢ ЩҶЩҮ ШӘЩӮЩҲЫҢЩ… Ш¬Щ„Ш§Щ„ЫҢ (ЫҢШ§ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ) ЩҲ ЩҶЩҮ ШіШ§Щ„ Ш§ЩҲЩ„ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҮЫҢЪҶ Ъ©ШҜШ§Щ… ЩҶЩ…ЫҢвҖҢШӘЩҲШ§ЩҶЩҶШҜ Щ…ШЁШҜШ§ Щ…ШӯШ§ШіШЁШ§ШӘ ЩҲШӘЩҶШ·ЫҢЩ… ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш¬ШҜЫҢШҜЫҢ ШЁШ§ШҙЩҶШҜ Ъ©ЩҮ ШЁШұШ§ЫҢ Ш§ЩҲЩ„ЫҢЩҶ ШЁШ§Шұ ШҜШұ ШіШ§Щ„ 1304 ЫҢШ№ЩҶЫҢ ЩҫШі Ш§ШІ ЪҜШ°ШҙШӘ 1303 ШіШ§Щ„ Ш§ШІ Щ…ШЁШҜШ§ ЩҮШ¬ШұШӘ ШЁЩҮ Щ…ШұШӯЩ„ЩҮ Ш§Ш¬ШұШ§ ШҜШұ ШўЩ…ШҜЩҮ Ш§ШіШӘ . ЩҲ ЩҮЩ…Ш§ЩҶ Ш·ЩҲШұ Ъ©ЩҮ ШҜШұ ШЁШ§Щ„Ш§ ЩҲ ЩҫЫҢШҙ Ш§ШІ Ш§ЫҢЩҶ ШҜШұ Ъ©ШӘШ§ШЁ В«ШІШұШҜШҙШӘ ЩҲ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢВ» ШўЩ…ШҜЩҮ Ш§ШіШӘ Щ…ШЁШҜШ§ ЩҲШ§ЩӮШ№ЫҢ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҮЩ…Ш§ЩҶШ§ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ -ШўШұЫҢШ§ЫҢЫҢ Ш§ШіШӘ Ъ©ЩҮ Щ…ШЁШҜШ§ ШўЩҶ 1128 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ЩҲ 507 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ Щ…ЫҢЩ„Ш§ШҜ Щ…ШіЫҢШӯ Ш§ШіШӘ.
ШЁЩҮ ЩҮЩ…ЫҢЩҶ ШҜЩ„ЫҢЩ„ ШЁШ§ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ вҖ“ ШўШұЫҢШ§ЫҢЫҢ ШұШ§ ШҜШұ Ш·ЩҲЩ„ 5000 ШіШ§Щ„ ШЁЩҮ ШөЩҲШұШӘ ШІЫҢШұ Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ЩҶЩҲШҙШӘ:
В ШҜЩҲШұЩҮ ШЁШІШұЪҜ 5000 ШіШ§Щ„ЩҮ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ ЩҲ Ш¬Ш§ЫҢЪҜШ§ЩҮ ШҜЩҲШұЩҮвҖҢЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ ШҜШұШўЩҶ
В
В
|
ШӘШұШӘЫҢШЁ |
ШўШәШ§ШІ |
ЩҫШ§ЫҢШ§ЩҶВ |
ШӘШұШӘЫҢШЁВ |
ШўШәШ§ШІВ |
ЩҫШ§ЫҢШ§ЩҶВ |
|
|
1 |
0 |
128 |
25 |
2697 |
2820 |
|
|
2 |
133 |
256 |
26 |
2825 |
2948 |
|
|
3 |
261 |
384 |
27 |
2953 |
3076 |
|
|
4 |
389 |
512 |
28 |
3081 |
3204 |
|
|
5 |
517 |
640 |
29 |
3209 |
3322 |
|
|
6 |
645 |
673 |
30 |
3327 |
3365 |
|
|
7 |
678 |
801 |
31 |
3370 |
3493 |
|
|
8 |
806 |
929 |
32 |
3498 |
3621 |
|
|
9 |
934 |
1057 |
33 |
3626 |
3749 |
|
|
10 |
1062 |
1185 |
34 |
3754 |
3877 |
|
|
11 |
1190 |
1313 |
35 |
3882 |
4005 |
|
|
12 |
1318 |
1346 |
36 |
4010 |
4038 |
|
|
13 |
1351 |
1474 |
37 |
4043 |
4166 |
|
|
14 |
1479 |
1620 |
38 |
4171 |
4294 |
|
|
15 |
1625 |
1730 |
39 |
4299 |
4422 |
|
|
В |
||||||
|
16 |
1735 |
1858 |
40 |
4427 |
4550 |
|
|
17 |
1863 |
1986 |
41 |
4555 |
4678 |
|
|
18 |
1991 |
2019 |
42 |
4683 |
4711 |
|
|
19 |
2024 |
2147 |
43 |
4716 |
4839 |
|
|
20 |
2152 |
2275 |
44 |
4844 |
4967 |
|
|
21 |
2280 |
2403 |
45 |
4972 |
5000 |
|
|
22 |
2408 |
2531 |
В |
|||
|
23 |
2536 |
2659 |
||||
|
24 |
2663 |
2692 |
||||
|
В |
В |
В | ||||
В
В
ШЁШҜЫҢЩҶ ШӘШұШӘЫҢШЁ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШҜЩҲШұЩҮ Ъ©Ш§Щ…Щ„ 5000 ШіШ§Щ„ЩҮ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ Щ…ШұЪ©ШЁ Ш§ШіШӘ Ш§ШІ ЩҮЩҒШӘ ШҜЩҲШұЩҮ 673ШіШ§Щ„ЩҮ ЩҲ ЫҢЪ© ЩҶЫҢЩ… ШҜЩҲШұЩҮ 289 ШіШ§Щ„ЩҮ. Ъ©ЩҮ ЩҮШұ ШҜЩҲШұЩҮ 673ШіШ§Щ„ЩҮ Ш®ЩҲШҜ Щ…ШұЪ©ШЁ Ш§ШіШӘ Ш§ШІ ЩҫЩҶШ¬ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁШ№Щ„Ш§ЩҲЩҮ ЫҢЪ© ШІЫҢШұ ШҜЩҲШұЩҮ 33 ШіШ§Щ„ЩҮ ЩҲ ЩҶЫҢЩ… ШҜЩҲШұЩҮ ЩҫШ§ЫҢШ§ЩҶЫҢ ЫҢШ§ ЩҮЩ…Ш§ЩҶ ЩҶЫҢЩ… ШҜЩҲШұЩҮ 289 ШіШ§Щ„ЫҢ Ъ©ЩҮ Ш®ЩҲШҜ Щ…ШұЪ©ШЁ Ш§ШіШӘ Ш§ШІ ШҜЩҲ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ ШЁШ№Щ„Ш§ЩҲЩҮ ЫҢЪ© ШІЫҢШұ ШҜЩҲШұЩҮ 33ШіШ§Щ„ЩҮ. ЩҲ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШҜШұ ЩҮШұШІЩ…Ш§ЩҶ ШЁЩҮ ШұШ§ШӯШӘЫҢ Щ…ЫҢ ШӘЩҲШ§ЩҶ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ ШұШ§ (ЩҫШі Ш§ШІ ШӘШЁШҜЫҢЩ„ ШЁЩҮ ЪҜШ§ЩҮШҙЩ…Ш§Шұ Ш§ЫҢШұШ§ЩҶЫҢ вҖ“ШўШұЫҢШ§ЫҢЫҢ) 673 ШіШ§Щ„ Ш¬ШҜШ§ ШіШ§Ш®ШӘ ШӘШ§ ШЁЩҮ Ъ©Щ…ШӘШұ Ш§ШІ 673 ШіШ§Щ„ ШұШіЫҢШҜ ЩҲ ШЁШұШ§ЫҢ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ 128 ШіШ§Щ„ Ъ©ЩҶШ§Шұ ЪҜШ°Ш§ШҙШӘ ШӘШ§ ШЁЩҮ ШұЩӮЩ…ЫҢ Ъ©Щ…ШӘШұ Ш§ШІ 128 ШіШ§Щ„ ШұШіЫҢШҜ ШӯШ§Щ„ Ш§ЪҜШұ Ш§ЫҢЩҶ ШұЩӮЩ… Ъ©Щ…ШӘШұШ§ШІ 128 ШіШ§Щ„ ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ ШҜШұ Ш¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ ЩҲШ¬ЩҲШҜ ШҜШ§ШҙШӘЩҮ ШЁШ§ШҙШҜ ШўЩҶ ШіШ§Щ„ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜШҢ ШҜШұ ШәЫҢШұ Ш§ЫҢЩҶ ШөЩҲШұШӘ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ ШЁЩҮ ЫҢЩӮЫҢЩҶ ЫҢЪ© ШіШ§Щ„ Ш№Ш§ШҜЫҢ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ.
ШЁЩҮ Ш·ЩҲШұ Щ…Ш«Ш§Щ„ Ш§ЪҜШұ ШЁШ®ЩҲШ§ЩҮЫҢЩ… ШЁШЁЫҢЩҶЫҢЩ… Ъ©ЩҮ ШіШ§Щ„ 458 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЫҢШ§ ШіШ§Щ„ ЩҲШ¶Ш№ Щ…ШЁШҜШ§ Ш¬Щ„Ш§Щ„ЫҢ ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҮ Ш§ШіШӘ ЫҢШ§ ЩҶЩҮШҢ ЩҫШі Ш§ШІ ШӘШЁШҜЫҢЩ„ ШўЩҶ ШЁЩҮ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ ШЁЩҮ ШӘЩҲШ¬ЩҮ ШЁЩҮ ШҜЩҲШұЩҮ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮ ШЁЩҮ ШҙШұШӯ ШІЫҢШұ Ш№Щ…Щ„ Щ…ЫҢ Ъ©ЩҶЫҢЩ…:
1586 = 1128 + 458
240 +(673Г—2 )=673Г·1586
112 +( 128Г—1 )=128Г· 240
В ЩҲ Ш§ШІ ШўЩҶШ¬Ш§ЫҢЫҢ Ъ©ЩҮ ШұЩӮЩ… ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ ЫҢШ§ Ш№ШҜШҜ112 ШҜШұШ¬ШҜЩҲЩ„ Ъ©ШЁЫҢШіЩҮ ЩҮШ§ЫҢ 128 ШіШ§Щ„ЩҮ ЩҲШ¬ЩҲШҜ ШҜШ§ШұШҜ ШЁЩҶШ§ШЁШұШ§ЫҢЩҶ Щ…ШҙШ®Шө Щ…ЫҢ ШҙЩҲШҜ Ъ©ЩҮ ШіШ§Щ„ 458 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ (1586Ш§ЫҢШұШ§ЩҶЫҢ) ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁЩҲШҜЩҮ Ш§ШіШӘ.В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В В
ЪҶЩҶЫҢЩҶ Ш§ШіШӘ Ъ©ЩҮ ШҜШұЩҶЩҮШ§ЫҢШӘ ШЁШ§ ШұШіЫҢШҜЩҶ ШЁЩҮ ШҜЩҲШұЩҮ Ъ©ШЁЫҢШіЩҮ 673 ШіШ§Щ„ЩҮ (ЫҢШ§ 163 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ Щ…ШҜШӘ 673ШіШ§Щ„) ЩҲ ЩҶЫҢШІ ШҜЩҲШұЩҮ Ъ©ШЁЫҢШіЩҮвҖҢЩҮШ§ЫҢ 128ШіШ§Щ„ЩҮ (31 ШЁШ§Шұ Ъ©ШЁЫҢШіЩҮ ШҜШұ ЩҮШұ 128ШіШ§Щ„) Щ…ЫҢвҖҢШӘЩҲШ§ЩҶ ШЁШ§ ЫҢЪ© ШұЩҲШҙ Ш№Щ„Щ…ЫҢ ЩҲШ№Щ…Щ„ЫҢ ШЁШұШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ (ШўШұЫҢШ§ЫҢЫҢ)ЩҫШұШҜШ§Ш®ШӘ.В
ЪҜЩҒШӘЩҶЫҢ Ш§ШіШӘ Ъ©ЩҮ ШЁШ№ШҜ Ш§ШІ ШұШіЫҢШҜЩҶ ШЁЩҮ ЪҶЩҶЫҢЩҶ ЩҶШӘЫҢШ¬ЩҮвҖҢШ§ЫҢ ШЁЩҲШҜВ Ъ©ЩҮ ШЁШ§ Щ…Ш№ШұЩҒЫҢ ШҜЩҲШіШӘЫҢ ШЁШ§ Ъ©ШӘШ§ШЁВ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ШҜЪ©ШӘШұ Щ…ЩҲШіЫҢ Ш§Ъ©ШұЩ…ЫҢ ШўШҙЩҶШ§ ШҙШҜЩ… ЩҲ Щ…Щ„Ш§ШӯШёЩҮ Ъ©ШұШҜЩ… Ъ©ЩҮ Ш§ЫҢШҙШ§ЩҶ ЩҶЫҢШІ ШЁЩҮ ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ Ъ©ШЁЫҢШіЩҮ ЪҜЫҢШұЫҢ ШЁШұ Ш§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ШұШ§ Щ…Ш·ШұШӯ ШіШ§Ш®ШӘЩҮ Ш§ЩҶШҜШҢ Ъ©ЩҮ Щ…ШӘШ§ШіЩҒШ§ЩҶЩҮ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· ЩҫЫҢШҙЩҶЩҮШ§ШҜЫҢ Ш§ЫҢШҙШ§ЩҶ ЫҢШ№ЩҶЫҢ 24219879/365 ШұЩҲШІ ШіШ§Щ„ 673В ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ЩҲ ШЁЩҮ Ш¬Ш§ЫҢ ШўЩҶ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„ 674 Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ ЪҶШұШ§ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ЩҲШұШҜ ЩҶШёШұ Ш§ЫҢШҙШ§ЩҶ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
9997 /162 = 24219879 /0 Г—673
В 2419 /163 = 24219879 /0 Г—674
ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШіШ§Щ„ 673 ЩҶЩ…ЫҢ ШӘЩҲШ§ЩҶШҜ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ЩҲ ШЁШ§ Ш·ЩҲЩ„ ШіШ§Щ„ Ш§ЩҶШӘШ®Ш§ШЁЫҢ Ш§ЫҢШҙШ§ЩҶ ШЁШ§ЫҢШҜ ШіШ§Щ„ 674 ШұШ§ Ъ©ШЁЫҢШіЩҮ ЪҜШұЩҒШӘ. ЩҲ Ш§ЫҢЩҶ Ъ©Ш§ШұЫҢ Ш§ШіШӘ Ъ©ЩҮ ШіШ§Щ„ ЩҮШ§ ЩҫЫҢШҙ Ш§ШӯЩ…ШҜ ШЁЫҢШұШҙЪ© Ш§ЩҶШ¬Ш§Щ… ШҜШ§ШҜЩҮ Ш§ШіШӘ. Ш§ЩҒШІЩҲЩҶ ШЁШұШ§ЫҢЩҶ ШЁШ§ ЪҶЩҶЫҢЩҶ Ш·ЩҲЩ„ Щ…ШӘЩҲШіШ· ШіШ§Щ„ Ш§ШӘЩҒШ§ЩӮЫҢ Ъ©ЩҮ ШЁШ§ЫҢШҜ ШҜШұ ШіШ§Щ„ 673 ШЁЫҢЩҒШӘШҜ ШҜШұ ШіШ§Щ„ 801 ШұШ® Ш®ЩҲШ§ЩҮШҜ ШҜШ§ШҜ.
ШЁШҜЫҢЩҶ ЪҜЩҲЩҶЩҮ Ъ©ЩҮ ШЁЩҮ Ш¬Ш§ЫҢ (802=128+674)Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ (801=128+673) ЫҢШ§ (801=127+674) Ъ©ЩҮ ШҜШұ ЩҮШұ ШҜЩҲ ШөЩҲШұШӘ ШЁЩҮ Ш¬Ш§ЫҢ Ш§ЫҢЩҶ Ъ©ЩҮ ШіШ§Щ„ 802 ЫҢЪ© ШіШ§Щ„ Ъ©ШЁЫҢШіЩҮ ШЁШ§ШҙШҜ ШіШ§Щ„ 801Ъ©ШЁЫҢШіЩҮ Ш®ЩҲШ§ЩҮШҜ ШЁЩҲШҜ ЩҲ ШҜШұ ШөЩҲШұШӘ Щ…ШӯШ§ШіШЁЩҮ Ш®ЩҲШ§ЩҮЫҢЩ… ШҜШ§ШҙШӘ:
1,
292959 = 24219879 /365В В Г—801
292193 = 24219879/ 365В Г—800
366 = 292193 вҖ“ 292959
Ш§ЩҒШІЩҲЩҶ ШЁШұШ§ЫҢЩҶ Ъ©ЩҮ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ Ш·ШЁЩӮ ШіЩҶШӘ ЩҲ Ш§ШіЩҶШ§ШҜ ЩҲ Щ…ШҜШ§ШұЪ© ШЁШ§ЩӮЫҢ Щ…Ш§ЩҶШҜЩҮ Ш§ШІ Щ…ЩҶШ¬Щ…Ш§ЩҶ ЪҜШ°ШҙШӘЩҮ ЩҮЩ…Ш§ЩҶ 2422/365 ШұЩҲШІ ЫҢШ§ 365 ШұЩҲШІ ЩҲ ЩҫЩҶШ¬ ШіШ§Ш№ШӘ ЩҲ 48 ШҜЩӮЫҢЩӮЩҮ ЩҲ 46 Ш«Ш§ЩҶЫҢЩҮ Щ…ЫҢвҖҢШЁШ§ШҙШҜ. Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ·ЫҢ Ъ©ЩҮ ШӯШӘЫҢ Ш§ШіШӯШ§ЩӮ ЩҶЫҢЩҲШӘЩҶ ШҜШ§ЩҶШҙЩ…ЩҶШҜ Щ…Ш№ШұЩҲЩҒ ЩҲ Ъ©Ш§ШҙЩҒ Ш¬Ш§Ш°ШЁЩҮ ШІЩ…ЫҢЩҶ ЩҶЫҢШІ ШҜШұ ШіШ§Щ„ 1700 Щ…ЫҢЩ„Ш§ШҜЫҢ ШЁШұШ§ЫҢ Ш§ШөЩ„Ш§Шӯ ШӘЩӮЩҲЫҢЩ… ЪҜШұЫҢЪҜЩҲШұЫҢШҢ ШҜШұ ЩҶШёШұ ШҜШ§ШҙШӘЩҮ Ш§ШіШӘ (ЫҢШ§ШҜШ§ШҙШӘ ЩҮШ§ЫҢ Щ…ЩҶШӘШҙШұ ЩҶШҙШҜЩҮ ЩҶЫҢЩҲШӘЩҶ). ЩҲ ЩҶЫҢШІ ШіЫҢЩ…ЩҲЩҶ ЩҶЫҢЩҲЪ©Щ…ШҢ ШіШӘШ§ШұЩҮ ШҙЩҶШ§Ші Щ…Ш№ШұЩҲЩҒ ШўЩ…ШұЫҢЪ©Ш§ЫҢЫҢ ШҜШұ ЩҒШұЩ…ЩҲЩ„ Щ…ШҙЩҮЩҲШұ Ш®ЩҲШҜ (ШҜШұШіШ§Щ„ 1900Щ…ЫҢЩ„Ш§ШҜЫҢ) Ш§ШіШ§Ші Щ…ШӯШ§ШіШЁШ§ШӘШҙ ШЁШұ ЩҫШ§ЫҢЩҮ ЩҮЩ…ЫҢЩҶ Ш·ЩҲЩ„ ШіШ§Щ„ Щ…ШӘЩҲШіШ· Ш®ЩҲШұШҙЫҢШҜЫҢ ЫҢШ№ЩҶЫҢ 2422/365 ШұЩҲШІ Ш§ШіШӘЩҲШ§Шұ Щ…ЫҢвҖҢШЁШ§ШҙШҜ.
ШҜШұ Ш®Ш§ШӘЩ…ЩҮ Ш§ШІШўЩҶ Ш¬Ш§ЫҢЫҢ Ъ©ЩҮ ШЁЫҢШҙ ШӘШұ Щ…ШұШҜЩ… ЩҒЩӮШ· ШЁШ§ ЪҜШ§ЩҮШҙЩ…Ш§Шұ ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ ШіШұЩҲ Ъ©Ш§Шұ ШҜШ§ШұЩҶШҜ ШҜШұ Ш§ЫҢЩҶ Ш¬Ш§ ШЁШұШ§ЫҢ ШіЩҮЩҲЩ„ШӘ Ъ©Ш§Шұ Ш¬ШҜЩҲЩ„ ШӘШ·ШЁЫҢЩӮЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§Шұ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ Щ…Ш№Ш§ШҜЩ„ ШўЩҶ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§Шұ Ш§ЫҢШұШ§ЩҶЫҢВ ШұШ§ ЫҢЪ© Ш¬Ш§ ЩҲ ШҜШұ ЩӮШ§Щ„ШЁ ЫҢЪ© Ш¬ШҜЩҲЩ„ ШЁШұШ§ШіШ§Ші ШҜЩҲШұЩҮ ЩҮШ§ЫҢ 673 ШіШ§Щ„ЩҮ ЩҲ 128 ШіШ§Щ„ЩҮШҢ Ш§ШІ ШўШәШ§ШІ ШӘЩӮЩҲЫҢЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ШӘШ§ ШіШ§Щ„ 1403 (ШіШ§Щ„ ЩҫШ§ЫҢШ§ЩҶ ШҜЩҲШұЩҮ 128 ШіШ§Щ„ЩҮ Щ…Ш№Ш§ШөШұ) ШҜШұ ШҜЩҲ ШұШҜЫҢЩҒ ЫҢЪ©ЫҢ ШЁШұШ§ЫҢ ЪҜШ§ЩҮШҙЩ…Ш§Шұ ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ ЩҲ ШҜЩҲЩ…ЫҢ ШЁШұШ§ЫҢ Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ Щ…Ш№Ш§ШҜЩ„ ШўЩҶ ШЁЩҮ ШөЩҲШұШӘ Щ…Ш¬ШІШ§ Щ…ЫҢвҖҢШўЩҲШұЫҢЩ…:
Ш¬ШҜЩҲЩ„ ШӘШ·ШЁЫҢЩӮЫҢ ШіШ§Щ„ ЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§ШІ ШўШәШ§ШІ ШӘШ§ ШіШ§Щ„ 1403ЩҮШ¬ШұЫҢ Ш®ЩҲШұШҙЫҢШҜЫҢ(2531Ш§ЫҢШұШ§ЩҶЫҢ)
В
В
|
В В ЩҫЩҶШ¬ ШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ |
ЪҶЩҮШ§ШұШіШ§Щ„ЩҮ В |
|
В |
В |
В |
В |
В |
В |
В |
В В |
|
В |
В |
В |
В |
В |
В |
В |
В В |
|
В |
В |
4 В В В 1132 |
8 В В В 1136 |
12 В В В 1140 |
16 1144 |
20 В 1148 |
24 В В В 1152 |
|
29 В В 1157 |
33 1161 |
37 1165 |
41 1169 |
45 1173 |
49 1177 |
53 1181 |
57 1185 |
|
62 1190 |
66 1194 |
70 1198 |
74 1202 |
78 1206 |
82 1210 |
86 1214 |
В В **** В В **** |
|
91 1219 |
95 1223 |
99 1227 |
103 1231 |
107 1235 |
111 1239 |
115 1243 |
119 1247 |
|
124 1252 |
128 1256 |
132 1260 |
136 1264 |
140 1268 |
144 1272 |
148 1276 |
152 1280 |
|
157 1285 |
161 1289 |
165 1293 |
169 1297 |
173 1301 |
177 1305 |
181 1309 |
185 1313 |
|
190 1318 |
194 1322 |
198 1326 |
202 1330 |
206 1334 |
210 1338 |
214 1342 |
218 1346 |
|
223 1351 |
227 1355 |
231 1359 |
235 1363 |
239 1367 |
243 1371 |
247 1375 |
В В **** В В **** |
|
252 1380 |
256 1384 |
260 1388 |
264 1392 |
268 1396 |
272 1400 |
276 1404 |
280 1408 |
|
285 1413 |
289 1417 |
293 1421 |
297 1425 |
301 1429 |
305 1433 |
309 1437 |
313 1441 |
|
318 1446 |
322 1450 |
326 1454 |
330 1458 |
334 1462 |
338 1466 |
342 1470 |
346 1474 |
|
351 1479 |
355 1483 |
359 1487 |
363 1491 |
367 1495 |
371 1499 |
375 1503 |
В В **** В В **** |
|
380 1508 |
384 1512 |
388 1516 |
392 1520 |
396 1524 |
400 1528 |
404 1532 |
408 1536 |
|
413 1541 |
417 1545 |
421 1549 |
425 1553 |
429 1557 |
433 1561 |
437 1565 |
441 1569 |
|
446 1574 |
450 1578 |
454 1582 |
458 1586 |
462 1590 |
466 1594 |
470 1598 |
474 1602 |
|
479 1607 |
483 1611 |
487 1615 |
491 1619 |
495 1623 |
499 1627 |
503 1631 |
В В **** В В **** |
|
508 1636 |
512 1640 |
516 1644 |
520 1648 |
524 1652 |
528 1656 |
532 1660 |
536 1664 |
|
541 1669 |
545 1673 |
549 1677 |
553 1681 |
557 1685 |
561 1689 |
565 1693 |
569 1697 |
|
574 1702 |
578 1706 |
582 1710 |
586 1714 |
590 1718 |
594 1722 |
598 1726 |
602 1730 |
|
607 1735 |
611 1739 |
615 1743 |
619 1747 |
623 1751 |
627 1755 |
631 1759 |
В В **** В В **** |
|
636 1764 |
640 1768 |
644 1772 |
648 1776 |
652 1780 |
656 1784 |
660 1788 |
664 1792 |
|
669 1797 |
673 1801 |
677 1805 |
681 1809 |
685 1813 |
689 1817 |
693 1821 |
697 1825 |
|
702 1830 |
706 1834 |
710 1838 |
714 1842 |
718 1846 |
722 1850 |
726 1854 |
730 1858 |
|
735 1863 |
739 1867 |
743 1871 |
747 1875 |
751 1879 |
755 1883 |
759 1887 |
В В **** В В **** |
|
764 1892 |
768 1896 |
772 1900 |
776 1904 |
780 1908 |
784 1912 |
788 1916 |
792 1920 |
|
797 1925 |
801 1929 |
805 1933 |
809 1937 |
813 1941 |
817 1945 |
821 1949 |
825 1953 |
|
830 1958 |
834 1962 |
838 1966 |
842 1970 |
846 1974 |
850 1978 |
854 1982 |
858 1986 |
|
863 1991 |
867 1995 |
871 1999 |
875 2003 |
879 2007 |
883 2011 |
887 2015 |
891 2019 |
|
896 2024 |
900 2028 |
904 2032 |
908 2036 |
912 2040 |
916 2044 |
920 2048 |
В В **** В В **** |
|
925 2053 |
929 2057 |
933 2061 |
937 2065 |
941 2069 |
945 2073 |
949 2077 |
953 2081 |
|
958 2086 |
962 2090 |
966 2094 |
970 2098 |
974 2102 |
978 2106 |
982 2110 |
986 2114 |
|
991 2119 |
995 2123 |
999 2127 |
1003 2131 |
1007 2135 |
1011 2139 |
1015 2143 |
1o19 2147 |
|
1024 2152 |
1028 2156 |
1032 2160 |
1036 2164 |
1040 2168 |
1044 2172 |
1048 2176 |
В В **** В В **** |
|
1053 2181 |
1057 2185 |
1061 2189 |
1065 2193 |
1069 2197 |
1073 2201 |
1077 2205 |
1081 2209 |
|
1086 2214 |
1090 2218 |
1094 2222 |
1098 2226 |
1102 2230 |
1106 2234 |
1110 2238 |
1114 2242 |
|
1119 2247 |
1123 2251 |
1127 2255 |
1131 2259 |
1135 2263 |
1139 2267 |
1143 2271 |
1147 2275 |
|
1152 2280 |
1156 2284 |
1160 2288 |
1164 2292 |
1168 2296 |
1172 2300 |
1176 2304 |
В В **** В В **** |
|
1181 2309 |
1185 2313 |
1189 2317 |
1193 2321 |
1197 2325 |
1201 2329 |
1205 2333 |
1209 2337 |
|
1214 2342 |
1218 2346 |
1222 2350 |
1226 2354 |
1230 2358 |
1234 2362 |
1238 2366 |
1242 2370 |
|
1247 2375 |
1251 2379 |
1255 2383 |
1259 2387 |
1263 2391 |
1267 2395 |
1271 2399 |
1275 2403 |
|
1280 2408 |
1284 2412 |
1288 2416 |
1292 2420 |
1296 2424 |
1300 2428 |
1304 2432 |
В В **** В В **** |
|
1309 2437 |
1313 2441 |
1317 2445 |
1321 2449 |
1325 2453 |
1329 2457 |
1333 2461 |
1337 2465 |
|
1342 2470 |
1346 2474 |
1350 2478 |
1354 2482 |
1358 2486 |
1362 2490 |
1366 2494 |
1370 2498 |
|
1375 2503 |
1379 2507 |
1383 2511 |
1387 2515 |
1391 2519 |
1395 2523 |
1399 2527 |
1403 2531 |
В
В
ШЁШ·ЩҲШұЫҢ Ъ©ЩҮ Щ…ШҙШ§ЩҮШҜЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ШҜШұ Ш¬ШҜЩҲЩ„ ШЁШ§Щ„Ш§ ШҜШұ ЩҮШұ ЫҢЪ© Ш§ШІ Ш¬Ш§ЫҢЪҜШ§ЩҮвҖҢЩҮШ§ЫҢ ШіШ§Щ„вҖҢЩҮШ§ЫҢ Ъ©ШЁЫҢШіЩҮ ШҜЩҲ ШұЩӮЩ… ЩҶЩҲШҙШӘЩҮ ШҙШҜЩҮ Ш§ШіШӘ Ъ©ЩҮ ЫҢЪ©ЫҢ ШЁШ§Щ„Ш§ШіШӘ ЩҲ ШҜЩҲЩ…ЫҢ ШҜШұ ШІЫҢШұ ШўЩҶШҢ Ъ©ЩҮ Ш§ШІ Ш§ЫҢЩҶ ШҜЩҲ ШұЩӮЩ…ШҢ ШұЩӮЩ… ШЁШ§Щ„Ш§ЫҢЫҢ ЩҶЩ…Ш§ЫҢШ§ЩҶЪҜШұ ШіШ§Щ„ ЫҢШ§ ШӘШ§ШұЫҢШ® ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш§ШіШӘ ЩҲ ШұЩӮЩ… ШІЫҢШұ ЩҶШҙШ§ЩҶЪҜШұ ЩҮЩ…Ш§ЩҶ ШіШ§Щ„ ЫҢШ§ ШӘШ§ШұЫҢШ® ШҜШұ ЪҜШ§ЩҮШҙЩ…Ш§ШұЫҢ Ш§ЫҢШұШ§ЩҶЫҢ Ш§ШіШӘ. ЩҲ ШЁЩҮ Ш·ЩҲШұЫҢ Ъ©ЩҮ Щ…Щ„Ш§ШӯШёЩҮ Щ…ЫҢвҖҢШҙЩҲШҜ ЩҶШ®ШіШӘЫҢЩҶ ШұЩӮЩ… ШҜШұ Ш¬ШҜЩҲЩ„ ШЁШ§Щ„Ш§ Ш№ШҜШҜ 4 Ш§ШіШӘ Ъ©ЩҮ Щ…ШЁЫҢЩҶ ШіШ§Щ„ ЪҶЩҮШ§ШұЩ… ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Ш§ШіШӘ Ъ©ЩҮ ШҜШұ ШөЩҲШұШӘ Ш§Ш¶Ш§ЩҒЩҮ Ъ©ШұШҜЩҶ ШұЩӮЩ… 1128 ШіШ§Щ„ ЩҫЫҢШҙ Ш§ШІ ЩҮШ¬ШұШӘ ( Щ…ШЁШҜШ§ Ш§ЫҢШұШ§ЩҶЫҢ ) ШЁШҜШ§ЩҶ Щ…ЫҢ ШҙЩҲШҜ 1132 ЩҲ ЩҮЩ…ЫҢЩҶ ЪҜЩҲЩҶЩҮ Ш§ШіШӘ ШЁЩӮЫҢЩҮ ШіШ§Щ„ ЩҮШ§ ШӘШ§ ШіШ§Щ„ 1403 ЩҮШ¬ШұЫҢ ШҙЩ…ШіЫҢ Щ…Ш№Ш§ШҜЩ„ 2531 Ш®ЩҲШұШҙЫҢШҜЫҢ Ш§Ш№ШӘШҜШ§Щ„ЫҢ Ш§ЫҢШұШ§ЩҶЫҢ
В





